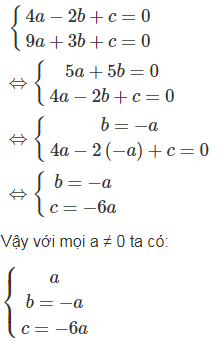Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Giải Sách Bài Tập Toán 9 Tập 2 !!
Tìm a, b, c để phương trình ax^2 + bx...
Tìm a, b, c để phương trình ax^2 + bx + c = 0 có hai nghiệm là x1 = -2
Câu hỏi :
Tìm a, b, c để phương trình a + bx + c = 0 có hai nghiệm là = -2 và = 3. Có thể tìm được bao nhiêu bộ ba số a, b, c thỏa mãn yêu cầu bài toán?
* Đáp án
* Hướng dẫn giải
x = -2 là nghiệm của phương trình: a + bx + c = 0, ta có:
4a - 2b + c = 0
x = 3 là nghiệm của phương trình: a + bx + c = 0 ta có:
9a + 3b + c = 0
Ba số a, b, c là nghiệm của hệ phương trình:
thì phương trình a + bx + c = 0 có nghiệm = -2; = 3
Ví dụ: a = 2, b = -2, c = -12 ta có phương trình:
2 - 2x - 12 = 0
⇒ - x - 6 = 0
⇒ (x + 2)(x - 3) = 0
Có nghiệm: = - 2; = 3
Có vô số bộ ba a, b, c thỏa mãn yêu cầu bài toán.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 9 Tập 2 !!
Số câu hỏi: 704
Copyright © 2021 HOCTAP247