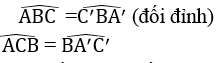Để giúp xe lửa chuyển từ một đường ray hướng này sang một đường ray
Câu hỏi :
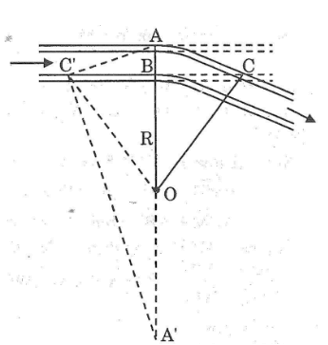
Để giúp xe lửa chuyển từ một đường ray hướng này sang một đường ray hướng khác người ta làm xen giữa một đoạn đường ray hìnhvòng cung (hình bên) .Biết chiều rộng của đường ray là AB ≈1,1m ,đoạn BC ≈ 28,4m.Hãy tính bán kính OA= R của đoạn đường ray hình vòng cung
* Đáp án
* Hướng dẫn giải
Xem đoạn đường ray thẳng là tiếp tuyến của hai đoạn đường ray vòng cung .
Điểm B cố định nằm trong đường tròn có cung là AC .Đường thẳng OB cắt đường tròn đó tại hai điểm A và A’
Ta có : A và A’ cố định
Vì B là tiếp điểm cung nhỏ trong nên BC là tiếp tuyến của đường tròn (O;OB)
Suy ra : BC ⊥ OB
Kéo dài BC cắt đường tròn (O;OA) tại C’
Suy ra : BC = BC’ ( đường kính vuông góc với dây cung)
Xét hai tam giác BAC và BC’A’ ta có:
(hai góc nội tiếp cùng chắn cung AC)
Suy ra BAC đồng dạng BC’A’
⇔ BC'/AB =BA'/BC ⇒ BC.BC’ = AB.A’B
Mà BC = BC’ và BA’ = 2R – AB
Nên = AB(2R –AB)
⇔ =1,1 (2R – 1,1)
⇔ 2,2R =806,56 + 1,21 =807,77
⇔ R = 807,77 : 2,2 ≈ 367,2(m)
Vậy bán kính đoạn đường ray hình vòng cung là 367,2m
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Giải Sách Bài Tập Toán 9 Tập 2 !!
Copyright © 2021 HOCTAP247