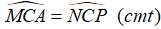Cho tam giác ABC có ba góc nhọn. Xác định vị trí của điểm M

* Hướng dẫn giải

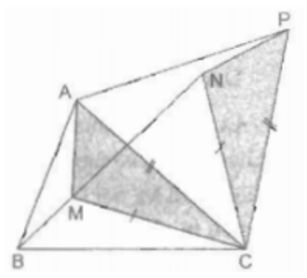
Trong $∆$ABC ta lấy điểm M. Nối MA, MB, MC.

Ta cần làm xuất hiện tổng MA + MB + MC sau đó tìm điều kiện để tổng đó nhỏ nhất.

Lấy MC làm cạnh dựng trên nửa mặt phẳng bờ BC chứa điểm A tam giác đều MCN. Suy ra: CM = MN.

Lấy AC làm cạnh dựng trên nửa mặt phẳng bờ AC không chứa điểm B tam giác đều APC. Khi đó, CA = CP

Xét $∆$AMC và $∆$PNC:

CM = CN (vì ΔMCN đều)

CA = CP (vì ΔAPC đều)

Suy ra: $∆$AMC = $∆$PNC (c.g.c)

⇒ PN = AM

MA + MB + MC = NP + MB + MN

Ta có $∆$ABC cho trước nên điểm P cố định nên BM + MN + NP ngắn nhất khi 4 điểm B, M, N, P thẳng hàng.