Cho đường thẳng (d): mx + 2y = 4 1. Vẽ đường thẳng khi m = 2 2. Tìm m để đường thẳng

* Hướng dẫn giải

1. Với m = 2, ta có $2\mathrm{x}+2\mathrm{y}=4\iff \mathrm{y}=-\mathrm{x}+2$

Với $\mathrm{x}=0\Rightarrow \mathrm{y}=2$, với $\mathrm{y}=0\Rightarrow \mathrm{x}=4$

Đồ thị hàm số y = -x + 4 là một đường thẳng đi qua (0;4) và (4;0) 

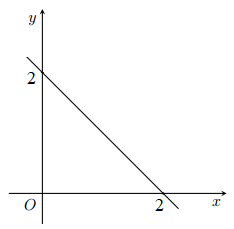
2. Xét phương trình $\mathrm{y}=-\frac{\mathrm{m}}{2}\mathrm{x}+2$. Ta có

a) (d) cắt hai trục tọa độ tại 2 điểm phân biệt $\iff -\frac{\mathrm{m}}{2}\ne 0\iff \mathrm{m}\ne 0$

b) (d) song song với Ox $\iff -\frac{\mathrm{m}}{2}=0\iff \mathrm{m}=0$

c) (d) song song với Oy $\iff \left\{\begin{array}{c}\mathrm{m}\ne 0\\ -\frac{2}{\mathrm{m}}=0\end{array}\right.$ (vô nghiệm)

Vậy không tồn tại m để (d) // Oy

d) (d) // $\mathrm{\Delta }\iff -\frac{\mathrm{m}}{2}=-1\iff \mathrm{m}=2$

e) (d) có hướng đi lên $\iff -\frac{\mathrm{m}}{2}>0\iff \mathrm{m}<0$

f) (d) có hướng đi xuống $\iff -\frac{\mathrm{m}}{2}<0\iff \mathrm{m}>0$

3. Giả sử là điểm cố định mà đường thẳng luôn đi qua. Khi đó ta có:

$$\begin{gathered} {\mathrm{mx}}_0+2{\mathrm{y}}_0=4\forall \mathrm{m}\iff \left\{\begin{array}{c}{\mathrm{x}}_0=0\\ 2{\mathrm{y}}_0-4=0\end{array}\right. \\ \iff \left\{\begin{array}{c}{\mathrm{x}}_0=0\\ {\mathrm{y}}_0=2\end{array}\right. \end{gathered}$$

Vậy M (0;2) là điểm cố định mà đường thẳng luôn đi qua khi m thay đổi.