Cho đường tròn (O) và một điểm M nằm bên ngoài đường tròn. Tia Mx quay quanh

* Hướng dẫn giải

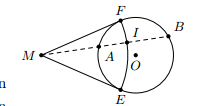
Phần thuận: Kẻ hai tiếp tuyến ME, MF tới đường tròn (O).

Ta có ${\mathrm{ME}}^2={\mathrm{MF}}^2=\mathrm{MA}.\mathrm{MB}={\mathrm{MI}}^2$ nên $\mathrm{ME}=\mathrm{MF}=\mathrm{MI}$

Suy ra I thuộc đường tròn (M; ME)

Hạn chế quỹ tích: vì A chỉ chạy trên cung $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (O) nên I chỉ chạy trên cung $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (M,ME) nằm trong đường tròn (O)

Phần đảo: lấy điểm I thuộc $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (M. ME) nằm trong đường tròn (O).

Nối MI cắt đường tròn (O) tại A và B. Ta cần chứng minh $\mathrm{MA}.\mathrm{MB}={\mathrm{MI}}^2$. Thật vậy, ${\mathrm{MI}}^2={\mathrm{ME}}^2=\mathrm{MA}.\mathrm{MB}$

Kết luận: vậy quỹ tích điểm I là cung $\stackrel{⏜}{\mathrm{EF}}$ của đường tròn (M, ME) nằm trong đường tròn (O).