Cho tam giác ABC vuông ở A, có cạnh BC cố định. Gọi I là giao điểm của ba đường

* Hướng dẫn giải

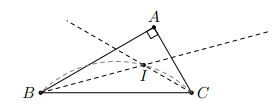
Phần thuận: Ta có:

Vì B, C cố định, A thay đổi, I luôn nhìn cạnh BC dưới một góc ${135}^0$ nên I di chuyển trên cung chứa góc ${135}^0$ dựng trên BC.

Phần đảo: Lấy điểm I là giao của cung chứa góc ${135}^0$ dựng trên BC và tia phân giác trong góc $\widehat{\mathrm{ACB}}$, ta chứng minh I cũng thuộc tia phân giác trong của góc $\widehat{\mathrm{ABC}}$.

Xét tam giác IBC, ta có:

Nên BI là phân giác trong của $∆\mathrm{ABC}$. Hay I là tâm đường tròn nội tiếp $∆\mathrm{ABC}$ (I là giao điểm của ba đường phân giác trong)

Giới hạn:

- Khi $\mathrm{I}\equiv \mathrm{B}$ thì ba điểm A, B, C thẳng hàng (trái giả thiết)

- Khi $\mathrm{I}\equiv \mathrm{C}$ thì ba điểm A, B, C thẳng hàng (trái giả thiết)

Vậy quỹ tích điểm I là cung chứa góc dựng trên cạnh BC đối xứng nhau qua BC, bỏ đi điểm B và C.

Kết luận: Quỹ tích điểm I là cung chứa góc ${135}^0$ dựng trên cạnh BC đối xứng nhau qua BC, bỏ đi điểm B và C.