Cho I, O lần lượt là tâm đường tròn nội tiếp, tâm đường tròn ngoại tiếp của

* Hướng dẫn giải

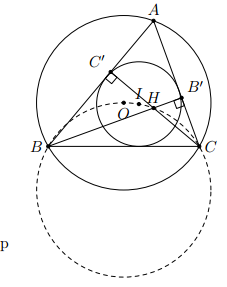
Xét tứ giác AB’HC’ ta có:

$$\begin{gathered} \widehat{\mathrm{B}\text{'}\mathrm{HC}\text{'}}={360}^0-\left(\hat{\mathrm{A}}+\hat{\mathrm{B}}+\hat{\mathrm{C}}\right) \\ ={360}^0-\left({60}^0+{90}^0+{60}^0\right)={120}^0 \\ \Rightarrow \widehat{\mathrm{BHC}}=\widehat{\mathrm{B}\text{'}\mathrm{HC}\text{'}}={120}^0 \end{gathered}$$

Xét $∆\mathrm{BIC}$ ta có:

$$\begin{gathered} \widehat{\mathrm{BIC}}={180}^0-\left(\widehat{\mathrm{BIC}}+\widehat{\mathrm{ICB}}\right) \\ ={180}^0-\left(\frac{\hat{\mathrm{B}}}{2}+\frac{\hat{\mathrm{C}}}{2}\right) \\ ={180}^0-\frac{1}{2}\left({180}^0-\hat{\mathrm{A}}\right)={120}^0 \end{gathered}$$

Như vậy, H và I đều nằm trên cung chứa góc ${120}^0$ dựng trên BC.

Mặt khác, $∆\mathrm{ABC}$ nội tiếp trong đường tròn tâm O nên góc nội tiếp $\widehat{\mathrm{BAC}}$ trong đường tròn (O) có số đo là

$$\begin{gathered} {60}^0=\widehat{\mathrm{BAC}}=\frac{1}{2}\mathrm{sd}\stackrel{⏜}{\mathrm{BC}}=\frac{1}{2}\widehat{\mathrm{BOC}} \\ \Rightarrow \widehat{\mathrm{BOC}}={120}^0 \end{gathered}$$

Vậy O nằm trên cung chứa góc ${120}^0$ dựng trên BC.

Nghĩa là 5 điểm B, C, O, I, H nằm trên cùng một đường tròn chứa cung chứa góc ${120}^0$ dựng trên BC.