Cho tam giác ABC vuông ở A. vẽ hai nửa đường tròn đường kính AB và AC

* Hướng dẫn giải

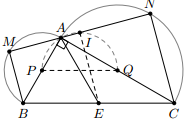
a) Vì M, N lần lượt nằm trên nửa đường tròn đường kính AB, AC nên $\widehat{\mathrm{BMA}}=\widehat{\mathrm{CNA}}={90}^0$

Do đó $\mathrm{BM}\perp \mathrm{MN}, \mathrm{CN}\perp \mathrm{MN}$ => BMCN là hình thang vuông (tại M, N)

b) Tìm quỹ tích trung điểm I của đoạn MN:

- Phần thuận:

Gọi E là trung điểm BC => IE là đường trung bình của hình thang BCNM

$\Rightarrow \mathrm{EI}\perp \mathrm{MN}$, do đó $\widehat{\mathrm{AIC}}={90}^0$

Vậy điểm M nằm trên đường tròn đường kính AE.

- Giới hạn:

Gọi P, Q lần lượt là trung điểm của AB, AC. Ta có APEQ là hình chữ nhật nên P, Q cùng nằm trên đường tròn đường kính AE.

+ Nếu $\mathrm{M}\equiv \mathrm{B}\Rightarrow \mathrm{I}\equiv \mathrm{P}$ 

+ Nếu $\mathrm{M}\equiv \mathrm{C}\Rightarrow \mathrm{I}\equiv \mathrm{C}$

Vậy điểm M chỉ nằm trên cung $\stackrel{⏜}{\mathrm{PQ}}$ của đường tròn đường kính AE.

- Phần đảo:

Lấy điểm I trên cung $\stackrel{⏜}{\mathrm{PQ}}$ của đường tròn đường kính AE. Nối AI lần lượt cắt  tại M, N.

Ta có $\widehat{\mathrm{AIE}}={90}^0$ (góc nội tiếp chắn nửa đường tròn) nên $\mathrm{EI}\perp \mathrm{MN}$ => EI // BM

Do đó EI là đường trung bình của hình thang BCNM => MI = NI

- Kết luận: quỹ tích điểm I nằm trên cung $\stackrel{⏜}{\mathrm{PQ}}$ của đường tròn đường kính AE.