Trang chủ
Đề thi & kiểm tra
Lớp 9
Toán học
Bài tập ôn tập chương 3 hình học 9 có đáp án !!
Cho tam giác ABC có góc A = 60 độ,...
Cho tam giác ABC có góc A = 60 độ, nội tiếp đường tròn (O). Trên cung nhỏ AC lấy
Câu hỏi :
Cho tam giác ABC có , nội tiếp đường tròn (O). Trên cung nhỏ AC lấy một điểm D, trên dây BD lấy điểm M sao cho DM = CD.
* Đáp án
* Hướng dẫn giải
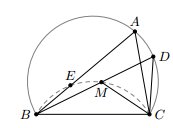
Vì nên
Do đó tam giác MDC đều (vì DM = DC)
b) Tìm quỹ tích điểm M:
- Phần thuận:
Vì tam giác MDC đều nên , do đó điểm M chạy trên cung chứa góc dựng trên đoạn BC.
- Giới hạn:
Gọi E là giao điểm của AB và cung chứa góc dựng trên đoạn BC.
+ nếu
+ nếu
Vậy điểm M chỉ nằm trên cung nhỏ của cung chứa góc dựng trên đoạn BC.
- Phần đảo:
Lấy điểm M trên cung nhỏ của cung chứa góc dựng trên đoạn BC. Nối BM cắt (O) tại D.
Ta có (góc nội tiếp) nên
Mà nên tam giác MCD đều, do đó DC = DM.
Kết luận: quỹ tích điểm M nằm trên cung nhỏ của cung chứa góc dựng trên đoạn BC.
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Bài tập ôn tập chương 3 hình học 9 có đáp án !!
Số câu hỏi: 182
Copyright © 2021 HOCTAP247
