Cho đường tròn (O) ngoại tiếp tam giác nhọn ABC. Gọi M và N lần lượt là

* Hướng dẫn giải

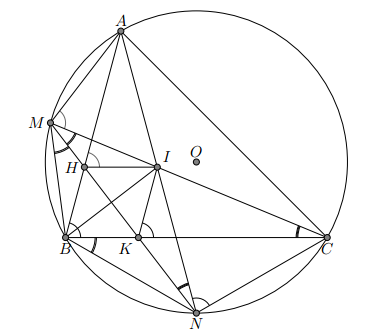
a) Ta có M là điểm chính giữa cung AB

$\Rightarrow \mathrm{AM}=\mathrm{BM}\Rightarrow \widehat{\mathrm{MNA}}=\widehat{\mathrm{MCB}}$$\Rightarrow \widehat{\mathrm{KNI}}=\widehat{\mathrm{ICK}}$

Tứ giác CNKI có C và N là hai đỉnh kề nhau cùng nhìn cạnh KI dưới hai góc bằng nhau nên CNKI nội tiếp (dấu hiệu nhận biết tứ giác nội tiếp).

Do dó bốn điểm C, N, I, K cùng thuộc một đường tròn.

b) Ta có N là điểm chính giữa cung BC

nên BK // HI (2)

Từ (1) và (2) suy ra tứ giác BHIK là hình bình hành.

Mặt khác, AN, CM lần lượt là các tia phân giác của các góc A và C trong tam giác ABC nên I là giao điểm ba đường phân giác, do đó BI là tia phân giác góc B.

Vậy tứ giác BHIK là hình thoi

Do vậy D, Q, C thẳng hàng nên KQ // PK.

Chứng minh tương tự ta có D, P, B thẳng hàng và DQ // PK.

Do đó tứ giác PDQK là hình bình hành nên E là trung điểm của PQ cũng là trung điểm của DK. Vậy D, E, K thẳng hàng.