Cho đường tròn tâm O và điểm A nằm ngoài đường tròn. Từ A kẻ hai

* Hướng dẫn giải

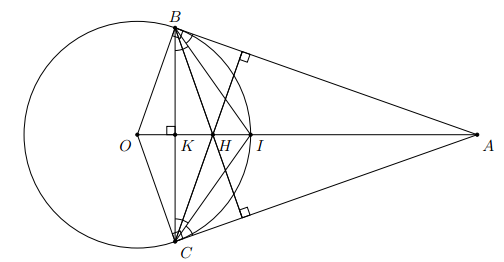
a) Vì AB, AC là các tiếp tuyến của (O) (tại B, C) nên $\widehat{\mathrm{ABO}}=\widehat{\mathrm{ACO}}=90°$

=> AOBC là tứ giác nội tiếp đường tròn đường kính AO.

Tương tự OC // BH  (2)

Từ (1) và (2) ta có BOCH là hình bình hành. Mà OB = OC nên BOCH là hình thoi.

Vì AB, AC là các tiếp tuyến của (O) nên AO là tia phân giác $\widehat{\mathrm{BAC}}$. Vì I là giao điểm của đoạn AO với (O) nên I là điểm chính giữa của cung (nhỏ) $\widehat{\mathrm{BC}}$

do vậy I là tâm đường tròn nội tiếp tam giác ABC.

c) Gọi I là giao điểm của OA và BC => K là trung điểm của BC và $\mathrm{BK}\perp \mathrm{AO}$

Áp dụng định lí Pitago cho tam giác AOB vuông tại B:

$\mathrm{AB}=\sqrt{{\mathrm{AO}}^2-{\mathrm{OB}}^2}=4\mathrm{cm}$

Áp dụng hệ thức lượng cho tam giác AOB vuông tại B: