Cho ba điểm cố định A, B, C thẳng hàng (B nằm giữa A và C). Gọi (O) là một

* Hướng dẫn giải

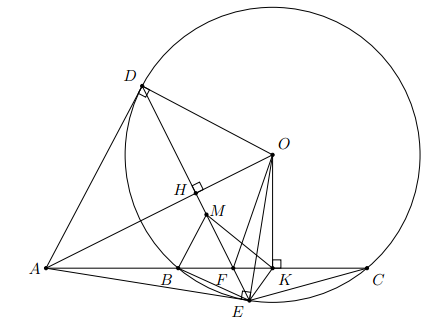
b) Dễ thấy, năm điểm O, A, D, E, K nằm trên đường tròn đường kính OA.

Vậy tứ giác BMKE là tứ giác nội tiếp.

c) Gọi F là giao điểm của DE và AC. Khi đó tứ giác OHFK nội tiếp đường tròn đường kính OF

Suy ra,

$\mathrm{AF}.\mathrm{AK}=\mathrm{AH}.\mathrm{AO}=$${\mathrm{AE}}^2=\mathrm{AB}.\mathrm{AC}$

Hay $\mathrm{AF}=\frac{\mathrm{AB}.\mathrm{AC}}{\mathrm{AK}}$, do đó F là điểm cố định. Vậy tâm đường tròn ngoại tiếp tam giác OHK chạy trên đường trung trực của đoạn thẳng FK.