Đề kiểm tra 15 phút - Đề số 1 - Bài 5, 6 - Chương 3 – Hình học 7
Tóm tắt bài
Đề bài
Cho tam giác ABC vuông tại A có \(\widehat B = {60^0}\). Trên cạnh BC lấy điểm H sao cho \(HB = AB\). Đường thẳng vuông góc với BC tại H cắt AC tại D.
a) Chứng minh rằng: BD là tia phân giác của góc ABC.
b) Chứng tỏ \(\Delta B{\rm{D}}C\) cân.
Hướng dẫn giải
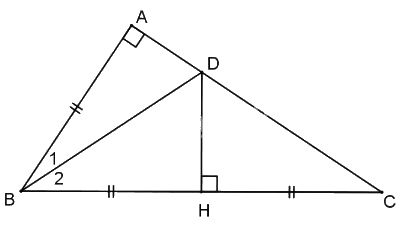
a) Xét hai tam giác vuông BAD và BHD có:
+) BD chung;
+) \(AB = HB\) (gt).
Do đó \(\Delta BA{\rm{D}} = \Delta BH{\rm{D}}\) (cạnh huyền – cạnh góc vuông)
\( \Rightarrow DA = DH\) (cạnh tương ứng), chứng tỏ D thuộc tia phân giác của góc \(\widehat {ABC}\).
b) Ta có \({\widehat B_1} = {\widehat B_2} = \dfrac{{\widehat {ABC}}}{ 2} =\dfrac {{{{60}^0}} }{2} = {30^0}.\)
Mặt khác \(\Delta ABC\) vuông tại A có \(\widehat B = {60^0}\) (gt) \( \Rightarrow \widehat C = {30^0} \Rightarrow {\widehat B_2} = \widehat C.\) Chứng tỏ \(\Delta ABC\) cân.
Copyright © 2021 HOCTAP247
