Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 5. Tính chất tia phân giác của một góc
Giải bài 32 trang 70 - Sách giáo khoa Toán 7 tập 2
Giải bài 32 trang 70 - Sách giáo khoa Toán 7 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác ABC. Chứng minh rằng giao điểm của hai tia phân giác của hai góc ngoài B1 và C1 (h.32) nằm trên tia phân giác của góc A.
Hướng dẫn giải
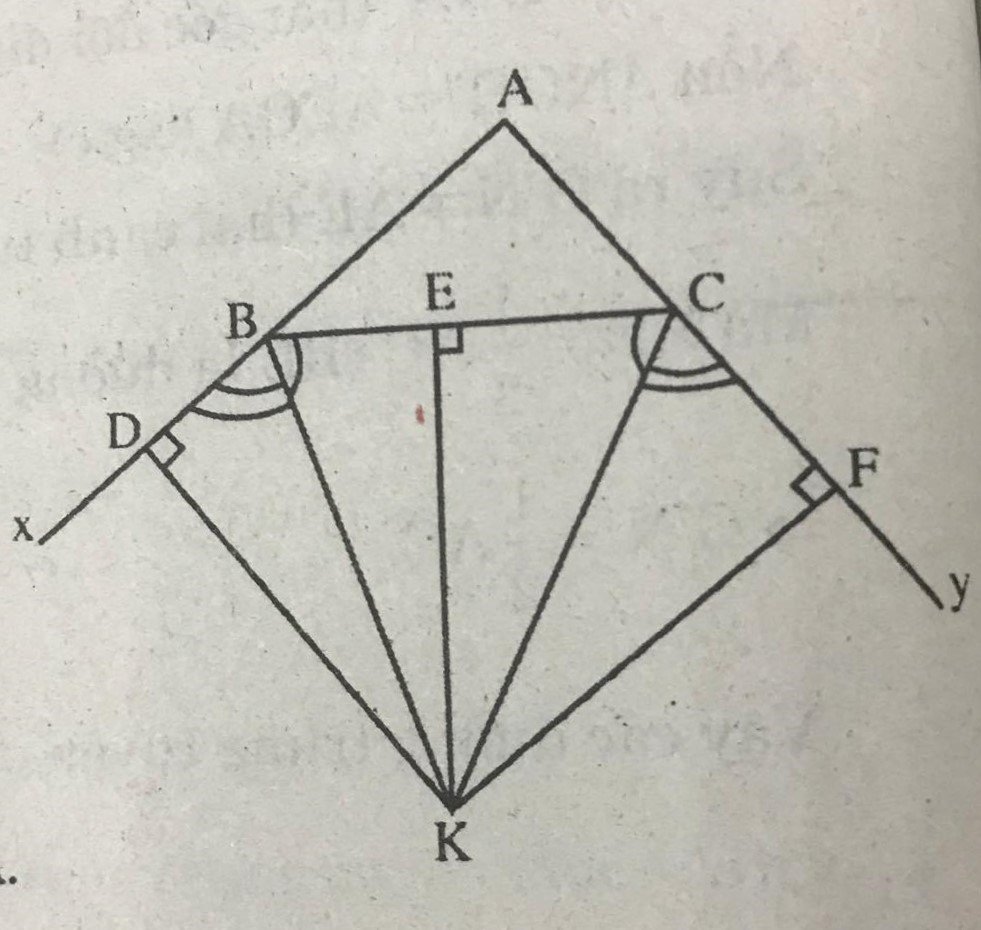
Gọi K là giao điểm của hai tia phân giác góc ngoài \(\widehat{CBx}\) và \(\widehat{BCy}\)
Kẻ KD \(\perp\) Bx , KE \(\perp\) BC , KF \(\perp\) Cy
K thuộc tia phân giác của góc \(\widehat{CBx}\)
=> KD = KE (tính chất tia phân giác) (1)
K thuộc tia phân giác góc \(\widehat{BCy}\)
=> KE = KF (tính chất tia phân giác) (2)
Từ (1) và (2) suy ra KD = KF
Do đó K thuộc tia phân giác của góc A (K cách đều hai cạnh của góc A)
Copyright © 2021 HOCTAP247
