Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 5. Tính chất tia phân giác của một góc
Đề kiểm tra 15 phút - Đề số 3 - Bài 5, 6 - Chương 3 – Hình học 7
Đề kiểm tra 15 phút - Đề số 3 - Bài 5, 6 - Chương 3 – Hình học 7
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác ABC . Chứng minh rằng: Hai đường phân giác của hai góc ngoài tại B và C và đường phân giác trong của góc A cùng đi qua một điểm.
Hướng dẫn giải
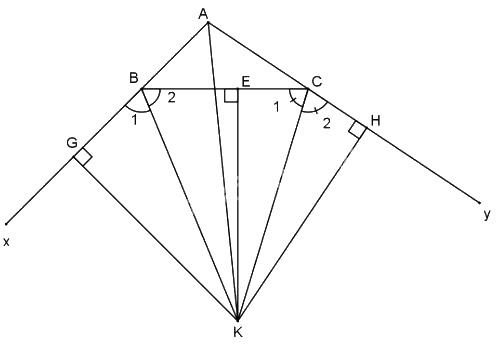
Gọi K là giao điểm hai phân giác góc ngoài tại đỉnh B và C. Kẻ KD, KE, KF lần lượt vuông góc với các đường thẳng AB, BC và AC. VÌ K thuộc phân giác của \(\widehat {CB{\rm{x}}}\) nên \(KD = KE\) (1); tương tự K thuộc phân giác của góc \(\widehat {BCy}\) nên \(KE = KF\) (2)
Từ (1) và (2) \( \Rightarrow K{\rm{D}} = KF\). Chứng tỏ K thuộc phân giác của góc BAC hay 3 đường phân giác trên cùng đi qua K.
Copyright © 2021 HOCTAP247
