Giải bài 34 trang 71 - Sách giáo khoa Toán 7 tập 2
Tóm tắt bài
Đề bài
Cho góc xOy khác góc bẹt. Trên tia Ox lấy hai điểm A và B, trên tia Oy lấy hai điểm C và D sao cho OA = OC, OB = OD. Gọi I là giao điểm của hai đoạn thẳng AD và BC. Chứng minh rằng:
a) BC = AD;
b) IA = IC, IB = ID;
c) Tia OI là tia phân giác của góc xOy.
Hướng dẫn giải
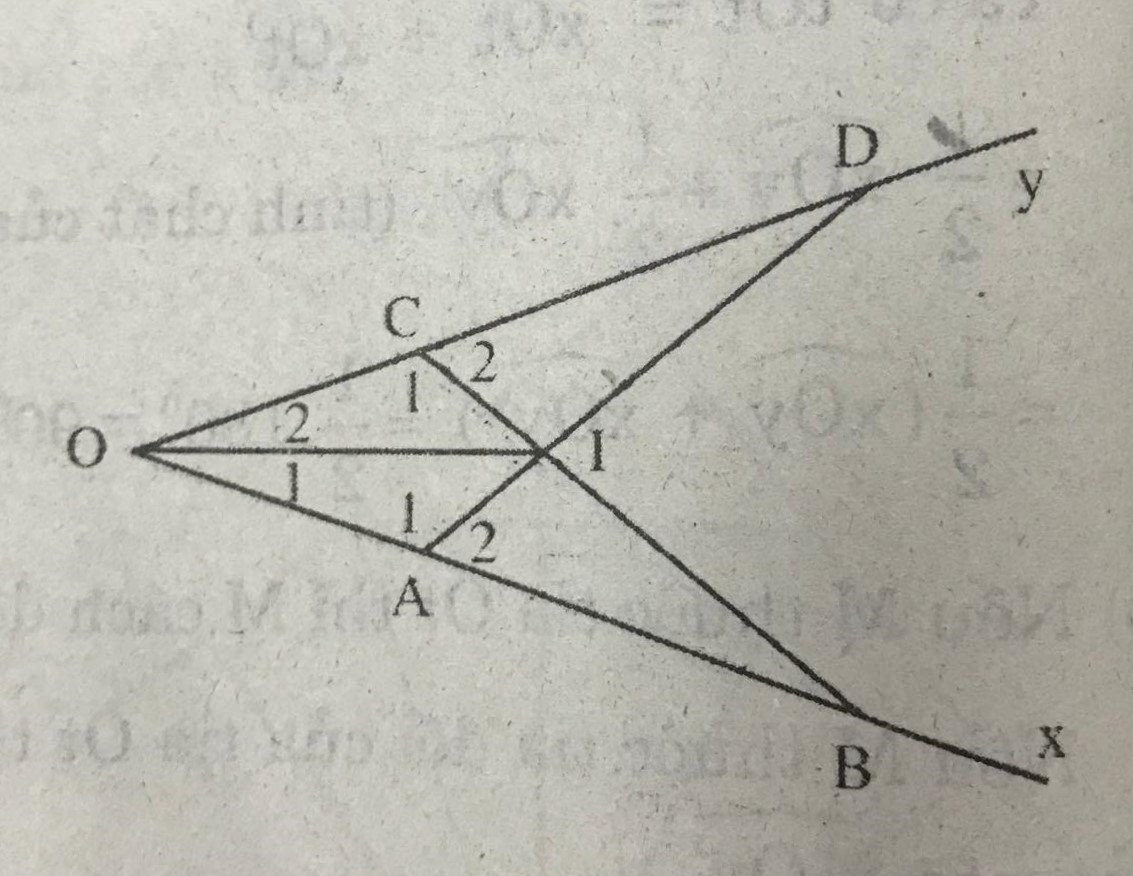
a) \(\triangle\)OBC và \(\triangle\)ODA có :
OB = OD (gt)
OA = OC (gt)
\(\widehat{O}\) là góc chung
Nên \(\triangle\)OBC = \(\triangle\)ODA (c.g.c)
Suy ra BC = AD
b) \(\triangle\)OBC = \(\triangle\)ODA (câu a)
=> \(\widehat{B}=\widehat{D}, \widehat{C_1}=\widehat{A_1}\)
\(\widehat{C_1}=\widehat{A_1} \Rightarrow \widehat{C_2}=\widehat{A_2}\) (hai góc kề bù của hai góc bằng nhau)
\(\triangle\)IAB và \(\triangle\)ICD có :
\(\widehat{A_2}=\widehat{C_2}, \widehat{B}=\widehat{D}\)
AB = CD (OB = OD, OA = OC)
Nên \(\triangle\)IAB = \(\triangle\)ICD (g.c.g)
Suy ra IA = IC , IB = ID (hai cạnh tương ứng)
c) \(\triangle\)IOA và \(\triangle\)IOC có :
IA = IC (câu b)
OA = OC (gt)
OI là cạnh chung
Nên \(\triangle\)IOA = \(\triangle\)IOC (c.c.c)
Suy ra \(\widehat{O_1}=\widehat{O_2} \Rightarrow OI\) là tia phân giác của góc \(\widehat{xOy}\)
Copyright © 2021 HOCTAP247
