Bài 54 trang 96 SGK Toán 8 tập 1

Đề bài

Cho góc vuông \(xOy\), điểm \(A\) nằm trong góc đó. Gọi \(B\) là điểm đối xứng với \(A\) qua \(Ox\), gọi \(C\) là điểm đối xứng với \(A\) qua \(Oy\). Chứng mình rằng điểm \(B\) đối xứng với điểm \(C\) qua \(O\).

Hướng dẫn giải

Áp dụng: +) Tính chất tam giác cân.

+) Tính chất hai điểm đối xứng qua 1 điểm.

Lời giải chi tiết

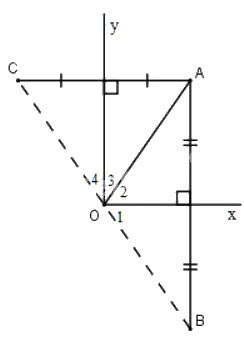
\(A\) đối xứng với \(B\) qua \(Ox\) (gt)và \(O\) nằm trên \(Ox\) (gt)

\( \Rightarrow \) \(OA\) đối xứng với \(OB\) qua \(Ox\)

 \( \Rightarrow \)  \(OA = OB\).  (1) (tính chất đối xứng)

\(\Rightarrow \Delta AOB\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow \) \(\widehat O_1=\widehat O_2\)   (3) (tính chất tam giác cân)

\(A\) đối xứng với \(C\) qua \(Oy\) (gt) và \(O\) nằm trên \(Oy\) (gt)

\( \Rightarrow \) \(OA\) đối xứng với \(OC\) qua \(Oy\) \( \Rightarrow \) \(OA = OC\)           (2)

\(\Rightarrow \Delta AOC\) cân tại \(O\) (dấu hiệu nhận biết tam giác cân)

\( \Rightarrow \) \(\widehat O_3=\widehat O_4\)    (4) (tính chất tam giác cân)

Từ (1) và (2) \( \Rightarrow \) \(OB = OC\)           (*)

Từ (3) và (4) \( \Rightarrow \) \(\widehat O_1+\widehat O_2+\widehat O_3+\widehat O_4\)\(=2(\widehat O_2+\widehat O_3)=2.90^0=180^0\) 

Do đó \(B, O, C\) thẳng hàng   (**)

Từ (*) và (**) \( \Rightarrow \) \(B\) đối xứng với \(C\) qua \(O\).