Bài 55 trang 96 SGK Toán 8 tập 1

Đề bài

Cho hình bình hành \(ABCD\), \(O\) là giao điểm của hai đường chéo. Một đường thẳng đi qua \(O\) cắt các cạnh \(AB\) và \(CD\) theo thứ tự ở \(M\) và \(N\). Chứng minh rằng điểm \(M\) đối xứng với điểm \(N\) qua \(O\).

Hướng dẫn giải

Áp dụng: +) Tính chất hình bình hành.

+) Tính chất hai điểm đối xứng qua 1 điểm.

Lời giải chi tiết

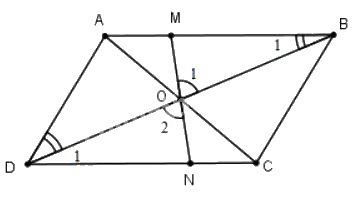
Vì \( ABCD\) là hình bình hành (gt)

\( \Rightarrow AB//DC\) (tính chất hình bình hành)

\( \Rightarrow\) \(\widehat{B_{1}}\) = \(\widehat{D_{1}}\) (so le trong)

Xét \(\Delta BOM\) và \(\Delta DON\) có:

 \(\widehat{B_{1}}\) = \(\widehat{D_{1}}\) (cmt)

 \(BO = DO\) (tính chất hình bình hành)

 \(\widehat{O_{1}}\) = \(\widehat{O_{2}}\) (đối đỉnh) 

\( \Rightarrow\) \( ∆BOM = ∆DON (g.c.g)\)

\( \Rightarrow\) \(OM = ON\) (hai cạnh tương ứng).

\( \Rightarrow\) \(O\) là trung điểm của \(MN\) (dấu hiệu nhận biết trung điểm)

\( \Rightarrow\) \(M \) đối xứng với \(N\) qua \(O\).