Bài 43 trang 128 SGK Toán 9 tập 1

Đề bài

Cho hai đường tròn(O; R) và (O’; r) cắt nhau tại A và \(B (R > r)\). Gọi I là trung điểm của OO’. Kẻ đường thẳng vuông góc với IA tại A, đường thẳng này cắt cá đường tròn tâm (O; R) và (O’; r) theo thứ tự tại C và D (khác A).

a) Chứng minh rằng AC = AD.

b) Gọi K là điểm đối xứng với điểm A qua điểm I. Chứng minh rằng KB vuông góc với AB

Hướng dẫn giải

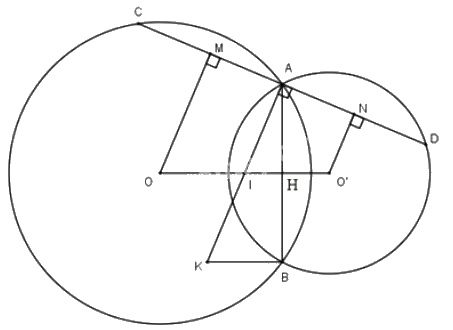
a) Vẽ OM ⊥ CD tại M, O’N ⊥CD tại N, ta có:

 \(MA = MC = {{AC} \over 2};\)

 \(NA = N{\rm{D}} = {{A{\rm{D}}} \over 2}\)

Mặt khác, ta có \(OM ⊥ CD, IA ⊥ CD, O’N ⊥ CD\)

\(⇒ OM // IA //O’N.\)

Hình thang OMNO’ (OM //O’N) có \(IA // OM; IO = IO’\) nên \(MA  = NA.\) Do vậy \(AC = AD\)

b) (O) và (O’) cắt nhau tại A, B

⇒ OO’ là đường trung trực của đoạn thẳng AB

\(⇒ IA = IB\)

Mặt khác \(IA = IK\) ( vì K đối xứng với A qua I)

Do đó: \(IA = IB = IK\)

Ta có ∆KBA có BI là đường trung tuyến và \(BI = {{AK} \over 2}\) nên ∆KBA vuông tại B

\(⇒ KB ⊥ AB\)