Đề kiểm tra 45 phút (1 tiết) - Đề số 5 - Chương 2 - Hình học 9

Đề bài

Cho đường tròn (O; R), lấy điểm A ở ngoài đường tròn (O) sao cho \(OA = 2R\). Từ A vẽ hai tiếp tuyến AB, AC đến đường tròn (O) với B, C là hai tiếp điểm.

a. Chứng minh rằng AO là đường trung trực của đoạn BC. Tính AB theo R.

b. Gọi I là trung điểm của đoạn OB, K là giao điểm của đoạn OA với đường tròn (O). Tính diện tích ∆OIK theo R.

c. Đường thẳng AI cắt cung lớn BC tại M. Tiếp tuyến tại M của đường tròn (O) cắt các đường thẳng AB, AC lần lượt tại P và Q. Chứng minh: \(MP = p – AQ\) (với p là nửa chu vi ∆APQ)

d. Chứng minh rằng diện tích ∆APQ bằng nửa chu vi của ∆APQ nhân với R.

Hướng dẫn giải

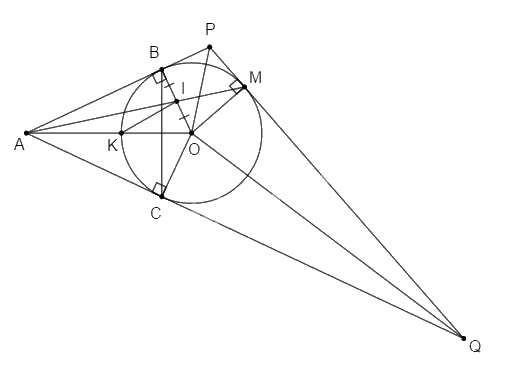
a. Ta có: \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau)

\(OB = OC (= R).\)

Do đó AO là đường trung trực của đoạn BC.

Ta có: \(AB ⊥ OB\) (tính chất tiếp tuyến)

\(⇒ ∆ABO\) vuông tại B, theo định lí Pi-ta-go, ta có:

\(AB = \sqrt {A{O^2} - B{O^2}}  = \sqrt {{{\left( {2R} \right)}^2} - {R^2}}  \)\(\,= R\sqrt 3 \)

b. Ta có: IK là đường trung bình của ∆AOB nên:

\(IK = {1 \over 2}AB = {{R\sqrt 3 } \over 2}\) và IK // AB, mà \(AB ⊥ OB ⇒ IK ⊥ OB.\)

Ta có: \({S_{OIK}} = {1 \over 2}IK.IO = {1 \over 2}.{{R\sqrt 3 } \over 2}.{R \over 2} = {{{R^2}\sqrt 3 } \over 8}\) (đvdt)

c. Ta có:

\(\eqalign{  p - AQ &= {{AP + PQ + AQ} \over 2} - AQ\cr& = {{AP + PQ + AQ - 2AQ} \over 2}  \cr  &  = {{AP + PQ - AQ} \over 2} \cr&= {{AB + BP + PM + MQ - CQ - AC} \over 2}  \cr  &  = {{BP + PM} \over 2} = {{2PM} \over 2} \cr&= PM\,\left( {đpcm} \right) \cr} \)

d. Ta có:

\(\eqalign{  & {S_{APQ}} = {S_{AOQ}} + {S_{QOP}} + {S_{POA}}  \cr  &  = {1 \over 2}R.AQ + {1 \over 2}R.QP + {1 \over 2}R.AP \cr&= {1 \over 2}R\left( {AQ + QP + AP} \right) \cr} \)