Đề kiểm tra 45 phút (1 tiết) - Đề số 9 - Chương 2 - Hình học 9
Tóm tắt bài
Đề bài
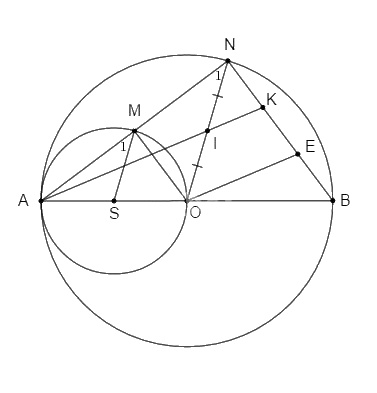
Cho đường tròn (O; R) đường kính AB. Gọi S là trung điểm của OA. Vẽ đường tròn tâm S đi qua A.
a. Chứng minh (O) và (S) tiếp xúc tại A.
b. Một đường thẳng đi qua A cắt (S) tại M và cắt (O) tại N (M, N khác A). Chứng minh : SM // ON
c. Chứng minh : OM // BN
d. Gọi I là trung điểm của ON, đường thẳng AI cắt BN tại K. Chứng minh: \(BK = 2NK\).
Hướng dẫn giải
a. Ta có: \(OS = OA – SA (d = R – R’)\)
Vậy (O) và (S) tiếp xúc trong tại A.
b. ∆ASM cân (\(SA = SM = R’\))
\( \Rightarrow {\widehat M_1} = \widehat {MAS}\)
Tương tự ∆AON cân
\(\eqalign{ & \Rightarrow {\widehat N_1} = \widehat {MAS} \cr & \Rightarrow {\widehat M_1} = {\widehat N_1} \cr} \)
Do đó SM // ON (đồng vị ).
c. Dễ thấy \(\widehat {AMO} = \widehat {ANB} = 90^\circ \) (góc chắn nửa đường tròn)
\(⇒ OM // BN (⊥ AN)\)
d. Kẻ OE // IK, ta có IK là đường trung bình của ∆ONE \(⇒ K\) là trung điểm của NE hay \(KN = KE.\)
Mặt khác trong ∆AKB ta có: OE là đường trung bình nên E là trung điểm của KB hay \(EK = EB\). Vậy \(BK = 2NK.\)
Cách khác : Gọi H là giao điểm của MO và AK, ta có: \(∆OIH = ∆NIK\) (g.c.g)
\(⇒ NK = OH\). Có O là trung điểm của AB, OH // BN (cmt)
\(⇒\) OH là đường trung bình của ∆AKB
\( \Rightarrow OH = {1 \over 2}KB\) hay \(2OH = BK\), mà \(OH = NK ⇒ 2NK = BK.\)
Copyright © 2021 HOCTAP247
