Giải bài 41 trang 128 - Sách giáo khoa Toán 9 tập 1
Tóm tắt bài
Đề bài
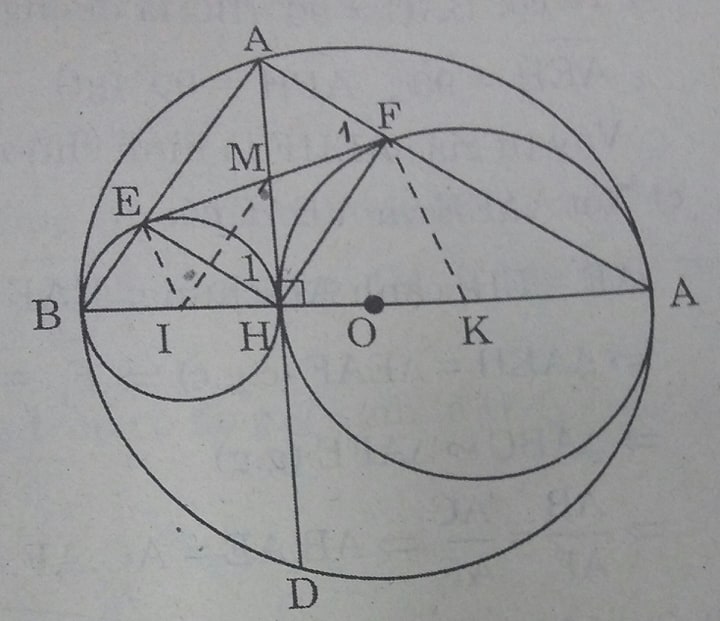
Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H.
Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBE, HCF.
a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).
b) Tứ giác AEHF là hình gì? Vì sao?
c) Chứng minh đẳng thức AE.AB = AF.AC
d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).
e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.
Hướng dẫn giải
Giải:
a) \(\Delta HBE\) vuông tại E nên tâm của đường tròn ngoại tiếp là trung điểm của BH.
Tương tự, tâm K của đường tròn ngoại tiếp \(\Delta HBE\) là trung điểm của HC.
Ta có: O\(I\)= OB- \(I\)B suy ra đường tròn (O) và đường tròn (I) tiếp xúc trong.
Chứng minh tương tự, đường tròn(O) và đường tròn (K) tiếp xúc trong.
Ta có: \(I\)K =\(I\)H +HK suy ra hai đường tròn (\(I\)) và (K ) tiếp xúc ngoài.
b) Ta có: \( \widehat{BAC}=90^0\) ( BC là đường kính và A thuộc đường tròn)
\(\widehat{AEH}=90^0 ; \widehat{AFH}= 90^0\)(gt)
Vậy tứ giác AEHF là hình chữ nhật ( có 3 góc vuông)
c) \(\Delta AEH\ và \ \Delta EAF\)
có AF= EH; cạnh AE chung; \(\widehat{EAF}=\widehat{AEH} \Rightarrow \Delta AEH = \Delta EAF (c.g.c)\)
\(\Rightarrow \widehat{F_1}=\widehat{H_1} \Rightarrow \widehat{F_1}= \widehat{B}\)
\( \Rightarrow \Delta ABC\ đồng\ dạng \ \Delta AFE(g.g)\)
\( \Rightarrow \frac{AB}{AF}= \frac{AC}{AE} \Rightarrow AB.AE= AC.AF\)
d) Gọi M là giao điểm của hai đường chéo AH và EF \( \Rightarrow\) ME= MH
\( \Rightarrow \Delta MEI = \Delta MHI (c.c.c) \Rightarrow \widehat{MEI}= \widehat{MHI}=90^0 \Rightarrow IE \perp EF\)
Vậy EF là tiếp tuyến của đường tròn (\(I\))
Chứng minh tương tự ta được EF là tiếp tuyến của đường tròn (K)
Vậy EF là tiếp tuyến chung của hai đường tròn (\(I\)) và (K)
e) Ta có \(EF= AH = \frac{1}{2}AD\) ( đường kính vuông góc với một dây thì chia đôi dây ấy)
Do EF lớn nhất \( \Leftrightarrow \) AD lớn nhất \( \Leftrightarrow \) AD là đường kính \( \Leftrightarrow \) H trùng với O
Vậy H trùng với O thì EF có độ dài lớn nhất.
Copyright © 2021 HOCTAP247
