Đề kiểm tra 45 phút (1 tiết) - Đề số 1 - Chương 2 - Hình học 9

Đề bài

Cho nửa đường tròn đường kính \(AB = 2R.\) Trên cùng nửa mặt phẳng bờ AB, vẽ hai tiếp tuyến Ax và By và  một tiếp tuyến tại M cắt hai tiếp tuyến Ax và By tại C và D.

a. Chứng minh: \(AC + BD = CD\) và AC.BD không đổi.

b. Chứng minh đường tròn đường kính CD tiếp xúc với AB.

c. Cho \(AC = {R \over 2}\). Tính MA, MB và bán kính đường tròn ngoại tiếp ∆BMD.

Hướng dẫn giải

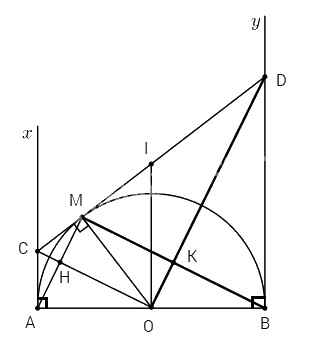
a. Ta có: \(CM = CA, DM = DB\) (tính chất hai tiếp tuyến cắt nhau)

mà \(CD = CM + MD \)\(⇒ CD = AC + BD\)

Lại có OC và OD lần lượt là hai phân giác của hai góc kề bù là \(\widehat {AOM}\) và \(\widehat {BOM} \Rightarrow \widehat {COD} = 90^\circ \)

Trong tam giác vuông COD có OM là đường cao nên ta có :

\(CM.DM = O{M^2} = {R^2}\) (không đổi)

\(⇒ AC.BD = {R^2}\)

b. Gọi I là tâm đường tròn đường kính CD, ta có OI là đường trung bình của hình thang vuông ACDB \(⇒\) OI // AC mà \(AC ⊥ AB\)

Do đó: \(IO ⊥ AB\) và \(IO = {{CA + BD} \over 2} = {{CD} \over 2} = IC,\) chứng tỏ đường tròn đường kính CD tiếp xúc với AB.

c. Ta có: \(OA = OM (=R), CA = CM\) (tính chất tiếp tuyến cắt nhau)

Do đó OC là đường trung trực của đoạn AM.

Gọi H là giao điểm của OC và AM.

Xét tam giác vuông CAO có đường cao AH, ta có:

\(\eqalign{   {1 \over {A{H^2}}}& = {1 \over {A{O^2}}} + {1 \over {C{A^2}}} \cr&= {1 \over {{R^2}}} + {1 \over {{{\left( {{R \over 2}} \right)}^2}}} \cr&= {1 \over {{R^2}}} + {4 \over {{R^2}}} = {5 \over {{R^2}}}  \cr  &  \Rightarrow AH = {{R\sqrt 5 } \over 5}\cr& \Rightarrow AM = {{2R\sqrt 5 } \over 5} \cr} \)

Ta có: \(\widehat {AMB} = 90^\circ \) (AB là đường kính), theo định lí Pi-ta-go :

\(BM = \sqrt {A{B^2} - A{M^2}} \)\(\; = \sqrt {{{\left( {2R} \right)}^2} - {{\left( {{{2R\sqrt 5 } \over 5}} \right)}^2}}  \)\(\;= \sqrt {4{R^2} - {{20{R^2}} \over {25}}}  = {{4R\sqrt 5 } \over 5}\)

Dễ thấy \(\widehat {OMD} = \widehat {OBD} = 90^\circ \) nên đường tròn ngoại tiếp ∆BMD có đường kính là OD.

Tứ giác MHOK là hình chữ nhật (K là giao điểm của OD và MB) nên \(OK = MH = {1 \over 2}AM = {{R\sqrt 5 } \over 5}\)

Xét tam giác vuông OMD, đường cao MK, ta có:

\(M{O^2} = OD.OK\) (hệ thức lượng)

\( \Rightarrow OD = {{M{O^2}} \over {OK}} = {{{R^2}} \over {{{R\sqrt 5 } \over 5}}} = R\sqrt 5 \)

Vậy bán kính đường tròn ngoại tiếp ∆BMD là \({{R\sqrt 5 } \over 2}\)