Trang chủ
Lớp 11
Toán Lớp 11 SGK Cũ
Ôn tập chương I - Hàm số lượng giác và phương trình lượng giác
Bài 10 trang 41 SGK Đại số và Giải tích 11
Bài 10 trang 41 SGK Đại số và Giải tích 11
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Phương trình \(2tanx – 2 cotx – 3 = 0\) có số nghiệm thuộc khoảng \(({{ - \pi } \over 2},\pi )\) là:
A. \(1\) B. \(2\) C. \(3\) D. \(4\)
Hướng dẫn giải
Đưa phương trình về dạng phương trình bậc hai của tanx, sử dụng công thức \(\cot x = \frac{1}{{\tan x}}\).
Lời giải chi tiết
Ta có:
\(\eqalign{
& 2\tan x - 2\cot x - 3 = 0 \cr
& \Leftrightarrow 2\tan x - {2 \over {\tan x}} - 3 = 0 \cr
& \Rightarrow 2{\tan ^2}x - 3\tan x - 2 = 0 \cr
& \Leftrightarrow \left[ \matrix{
\tan x = 2 \hfill \cr
\tan x = {{ - 1} \over 2} \hfill \cr} \right. \cr} \)
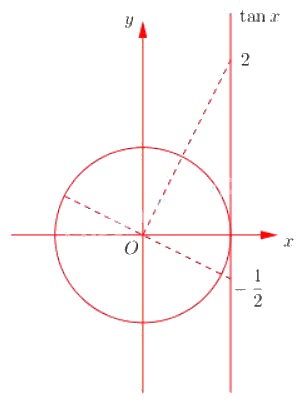
Vẽ đường tròn lượng giác với giá trị \(tanx = 2\), \(\tan x = {{ - 1} \over 2}\) ta thấy phương trình có ba nghiệm thuộc khoảng .
Chọn đáp án C.
Copyright © 2021 HOCTAP247
