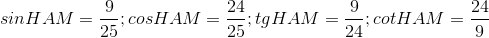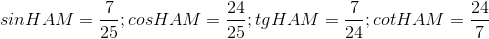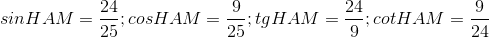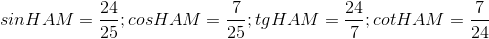Biến đổi đơn giản biểu thức chứa tỉ số lượng giác

A

B

C

D

A \(\begin{array}{l}\sin ABD = \frac{{2\sqrt 5 }}{5}\\\cos ABD = \frac{\sqrt 5}{{5 }}\\\tan ABD = 2\\\cot ABD = \frac{1}{2}\end{array}\)

B \(\begin{array}{*{20}{l}}
{\sin ABD = \frac{{2\sqrt {11} }}{{11}}}\\
{\cos ABD = \frac{{\sqrt {11} }}{{11}}}\\
{\tan ABD = 2}\\
{\cot ABD = \frac{1}{2}}
\end{array}\)

C \(\begin{array}{*{20}{l}}
{\sin ABD = \frac{{\sqrt {11} }}{{11}}}\\
{\cos ABD = \frac{{2\sqrt {11} }}{{11}}}\\
{\tan ABD = \frac{1}{2}}\\
{\cot ABD = 2}
\end{array}\)

D \(\begin{array}{*{20}{l}}
{\sin ABD = \frac{{\sqrt 5 }}{5}}\\
{\cos ABD = \frac{{2\sqrt 5 }}{5}}\\
{\tan ABD = \frac{1}{2}}\\
{\cot ABD = 2}
\end{array}\)

A 0

B 1

C 2

D -1

A a) \(\sin C = \frac{{\sqrt 6 }}{3};\,\,\,\cos C = \frac{{\sqrt 3 }}{3}\)

\(\tan C = \sqrt 2 ;\,\,\,\cot C = \frac{{\sqrt 2 }}{2}\)

b) \(AC = 6;\,\,BC = 3\sqrt 6 ;\,\,AB = 3\sqrt 2 \)

B a) \(\sin C = \frac{{\sqrt 6 }}{3};\,\,\,\cos C = \frac{{\sqrt 3 }}{3}\)

\(\tan C = \sqrt 2 ;\,\,\,\cot C = \frac{{\sqrt 2 }}{2}\)

b) \(AC = 6;\,\,BC = 3\sqrt 2 ;\,\,AB = 2\sqrt 3 \)

C a) \(\sin C = \frac{{\sqrt 3 }}{3};\,\,\,\cos C = \frac{{\sqrt 6 }}{3}\)

\(\tan C = \frac{1}{{\sqrt 2 }};\,\,\,\cot C = \sqrt 2 \)

b) \(AC = 6;\,\,BC = 3\sqrt 6 ;\,\,AB = 3\sqrt 2 \)

D a) \(\sin C = \frac{{\sqrt 3 }}{3};\,\,\,\cos C = \frac{{\sqrt 6 }}{3}\)

\(\tan C = \frac{1}{{\sqrt 2 }};\,\,\,\cot C = \sqrt 2 \)

b) \(AC = 6;\,\,BC = 3\sqrt 2 ;\,\,AB = 2\sqrt 3 \)

A -2

B 1

C 0

D -1

A \(-2\)

B \(-1\)

C \(1\)

D \(2\)

A \(\cos \alpha  = \frac{{\sqrt 5 }}{3};\,\,\tan \alpha  =  - \frac{2}{3};\,\,\cot \alpha  =  - \frac{{\sqrt 5 }}{2}\)

B \(\cos \alpha  = \frac{{\sqrt 5 }}{3};\,\,\tan \alpha  = \frac{{2\sqrt 5 }}{5};\,\,\cot \alpha  = \frac{{\sqrt 5 }}{2}\)

C \(\cos \alpha  = \frac{{\sqrt 2 }}{3};\,\,\tan \alpha  = \sqrt 2 ;\,\,\cot \alpha  = \frac{1}{2}\)

D \(\cos \alpha  = \frac{1}{3};\,\,\tan \alpha  = 2;\,\,\cot \alpha  = \frac{1}{2}\)