Bài 52 trang 128 SGK Toán 7 tập 1
Tóm tắt bài
Đề bài
Cho góc xOy có số đo \(120^0\), điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox (B thuộc Ox), kẻ AC vuông góc với Oy (C thuộc Oy). Tam giác ABC là tam giác gì ? Vì sao?
Hướng dẫn giải
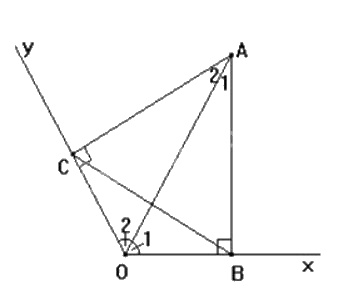
Tam giác ACO vuông tại C
Tam giác ABO vuông tại B
Xét hai tam giác vuông ACO và ABO có:
+) \(\widehat{O_{1}}=\widehat{O_{2}}\) (Vì OA là tia phân giác góc xOy)
+) AO chung
Suy ra \(∆ACO=∆ABO\) (cạnh huyền-góc nhọn)
Suy ra \(AC=AB\) (hai cạnh tương ứng)
\(\widehat {{A_1}} = \widehat {{A_2}}\) (hai góc tương ứng)
\(\widehat {{O_1}} = {1 \over 2}\widehat {xOy} = {1 \over 2}{.120^0} = {60^0}\) (Vì OA là tia phân giác góc xOy)
Áp dụng định lí tổng ba góc trong một tam giác vào \(\Delta OBA\) ta có:
\(\eqalign{
& \widehat {{O_1}} + \widehat B + \widehat {{A_1}} = {180^0} \cr
& \Rightarrow \widehat {{A_1}} = {180^0} - \widehat {{O_1}} - \widehat B \cr&\;\;\;\;\;\;\;\;\;\;= {180^0} - {60^0} - {90^0} = {30^0} \cr} \)
Do đó: \(\widehat {{A_1}} = \widehat {{A_2}} = {30^0}\)
Hay \(\widehat {BAC} = \widehat {{A_1}} + \widehat {{A_2}} = {60^0}\)
Vây \(∆ABC\) có \(AC=AB\) và \(\widehat {BAC}= {60^0}\) nên là tam giác đều
Copyright © 2021 HOCTAP247
