Đề kiểm tra 15 phút - Đề số 4 - Bài 6 - Chương 2 - Hình học 7
Tóm tắt bài
Đề bài
Cho tam giác ABC, tia phân giác của góc C cắt AB ở D. Trên tia đối của tia CA lấy điểm E sao cho CE = CB.
a) Chứng minh CD // EB.
b) Tia phân giác của góc E cắt đường thẳng CD tại F, vẽ \(CK \bot EF\) tại K. Chứng minh CK là tia phân giác của góc ECF.
Hướng dẫn giải
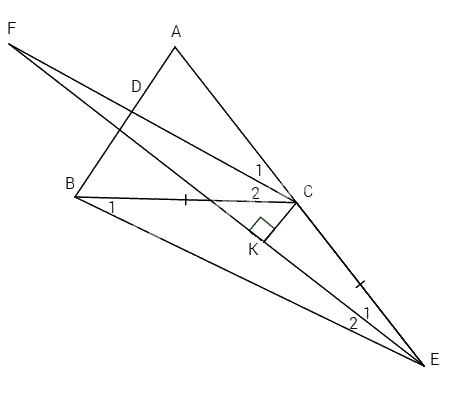
a) Ta có CE = CB (giả thiết) nên \(\Delta BCE\) cân \( \Rightarrow \widehat {{B_1}} = \widehat E\)
CD là tia phân giác của góc C (giả thiết) \( \Rightarrow \widehat {{C_1}} = \widehat {{C_2}}\)
Mà ACB là góc ngoài của \(\Delta BCE\) \( \Rightarrow \widehat {ACB} = \widehat {{B_1}}\) hay \(\widehat {{B_1}} = \widehat {{C_2}}.\)
Do đó CD // EB (cặp góc so le trong bằng nhau).
b) Ta có CF // BE (chứng minh trên) \( \Rightarrow \widehat {CEF} = \widehat {{E_2}}\) (cặp góc so le trong) mà \(\widehat {{E_1}} = \widehat {{E_2}}\) (giả thiết) \( \Rightarrow \widehat {CFE} = \widehat {{E_1}}\).
Do đó \(\Delta CFE\) cân tại C \( \Rightarrow CF = CE\).
Lại có \(CK \bot EF\) (giả thiết) nên \(\Delta CKF = \Delta CKE\) (g.c.g)
\( \Rightarrow \widehat {FCK} = \widehat {CEK}\) hay CK là tia phân giác của \(\widehat {ECF}\).
Copyright © 2021 HOCTAP247
