Giải bài 52 trang 128 - Sách giáo khoa Toán 7 tập 1

Đề bài

Cho góc xOy có số đo 120o điểm A thuộc tia phân giác của góc đó. Kẻ AB vuông góc với Ox, kẻ AC vuông góc với Oy. Tam giác ABC là tam giác gì ? Vì sao?

Hướng dẫn giải

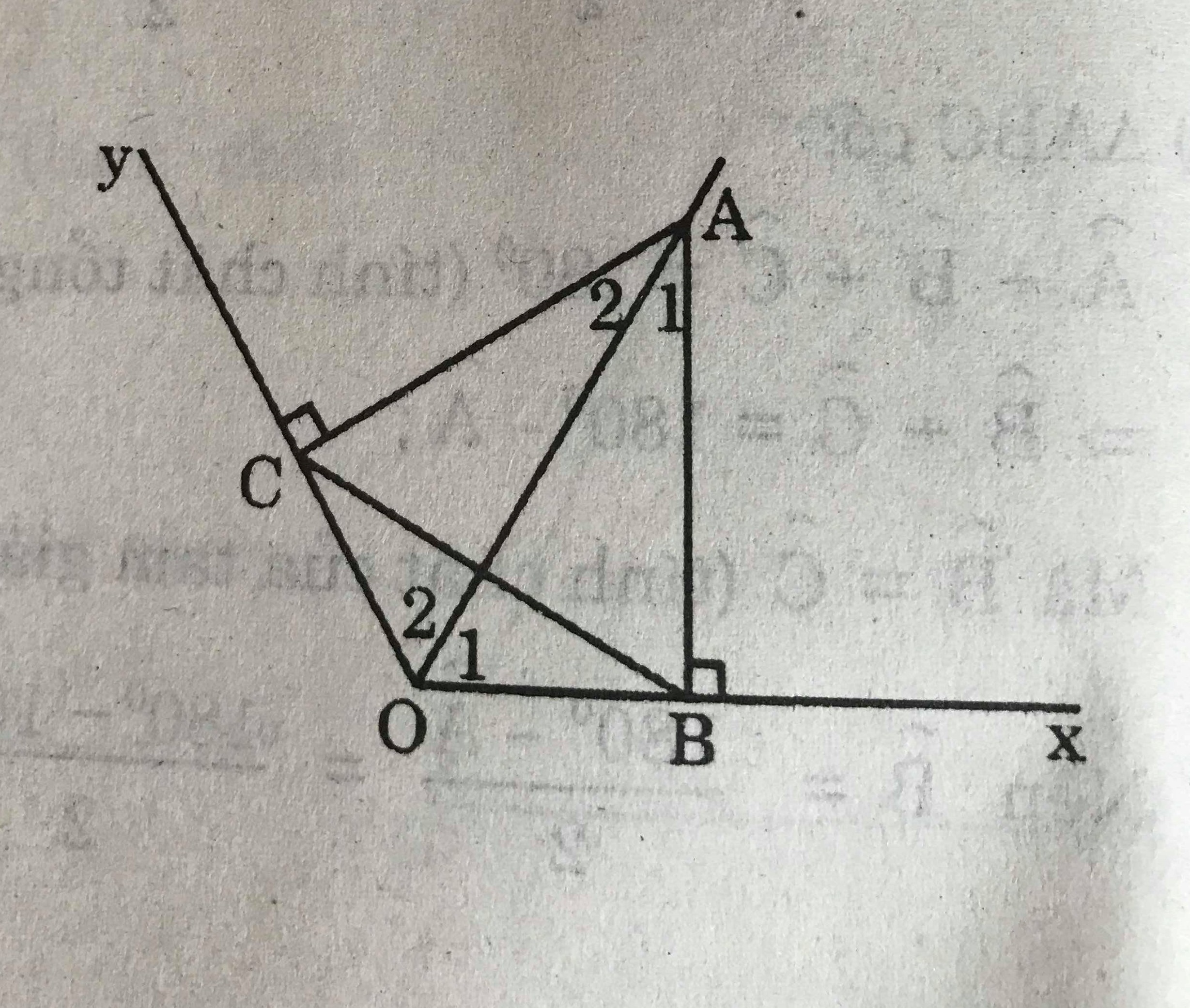
Xét hai tam giác vuông ΔAOB và ΔAOC có :

\(\widehat{O_1}=\widehat{O_2}\) ( OA là tia phân giác \(\widehat{xOy}\) )

OA là cạnh chung

Nên ΔAOB = ΔAOC (cạnh huyền - góc nhọn)

=> AB = AC

=> ΔABC cân tại A         (1)

Ta có : \(\widehat{O_1}=\widehat{O_2}\)\(=\dfrac{\widehat{xOy}}{2} = \dfrac{120^0}{2} = 60^0\) (OA là tia phân giác của \(\widehat{xOy}\))

Nên \(\widehat{A_1}=\widehat{A_2} =30^0\) (cùng phụ góc \(60^0\) )

=> \(\widehat{BAC} = 60^0\)

Từ (1) và (2) suy ra ΔABC là tam giác đều.