Giải bài 51 trang 128 - Sách giáo khoa Toán 7 tập 1

Đề bài

Cho tam giác ABC cân tại A. Lấy điểm D thuộc cạnh AC, điểm E thuộc cạnh AB sao cho AD = AE

b) Gọi I là giao điểm của BD và CE. ΔIBC là tam giác gì ? Vì sao ?

Hướng dẫn giải

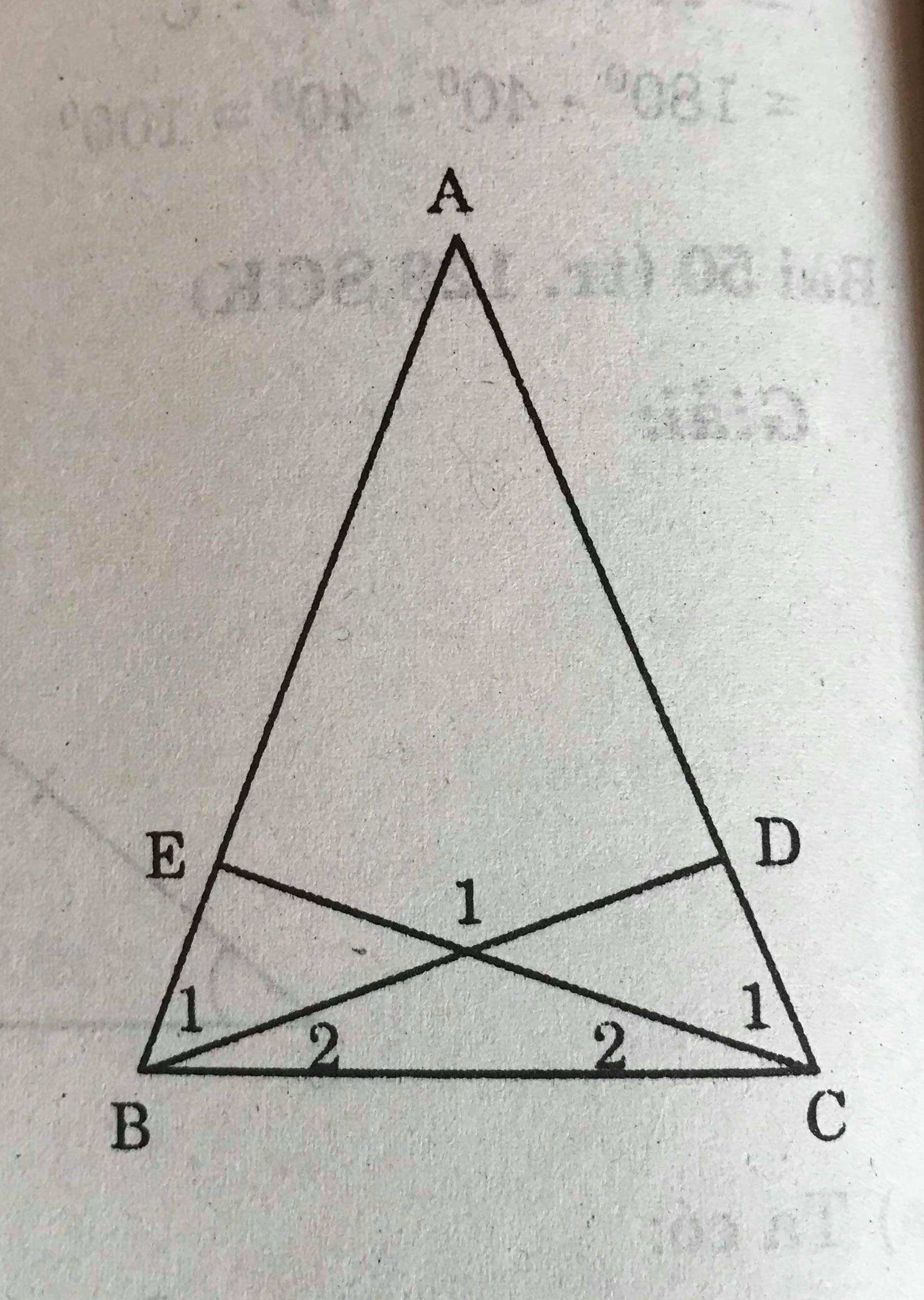
a) Xét hai tam giác \(\triangle\)ABD và \(\triangle\)ACE có :

AD = AE (gt)

AB = AC (\(\triangle\)ABC cân tại A)

\(\widehat{A}\) là góc chung

Nên \(\triangle\)ABD = \(\triangle\)ACE (c.g.c)

=> \(\widehat{ABD}\) = \(\widehat{ACE}\)

b) \(\triangle\)ABC cân tại A => \(\widehat{B}\) = \(\widehat{C}\)

=> \(\widehat{B}\) - \(\widehat{B_1}\) = \(\widehat{C}\) - \(\widehat{C_1}\) ( \(\widehat{B_1}\) = \(\widehat{C_1}\) )

=> \(\widehat{B_2}\) = \(\widehat{C_2}\)

=> \(\triangle\)IBC cân tại I