Bài 29 trang 67 SGK Toán 7 tập 2

Đề bài

Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng:

                   GA = GB = GC.

Hướng dẫn: Áp dụng định lí ở bài tập 26.

Hướng dẫn giải

Áp dụng định lí ở bài tập 26: Trong một tam giác cân, hai đường trung tuyến ứng với hai cạnh bên thì bằng nhau.

Lời giải chi tiết

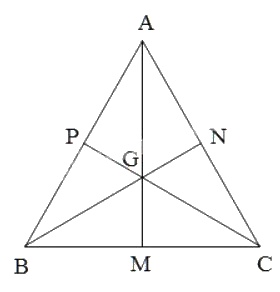
Gọi M, N, P lần lượt là trung điểm của các cạnh BC, AC, AB.

Vì ∆ABC là tam giác đều nên AB = AC = BC. 

Xét ∆ABC có AB = AC nên ∆ABC cân tại A

\( \Rightarrow \) BN = CP (hai trung tuyến bằng nhau theo định lí ở bài tập 26)

và GB = GC = \(\frac{2}{3}\) BN (= \(\frac{2}{3}\) CP)   (1)

Xét ∆ABC có BA = BC nên ∆ABC cân tại B

\( \Rightarrow \)  CP = AM  (hai trung tuyến bằng nhau theo định lí ở bài tập 26)

và GC = GA = \(\frac{2}{3}\) CP (= \(\frac{2}{3}\) AM)   (2)

Từ (1) và (2) ta suy ra: GA = GB = GC (đpcm).