Giải bài 27 trang 67 - Sách giáo khoa Toán 7 tập 2

Đề bài

Hãy chứng minh định lí đảo của định lí trên: Nếu tam giác có hai đường trung tuyến bằng nhau thì tam giác đó cân.

Hướng dẫn giải

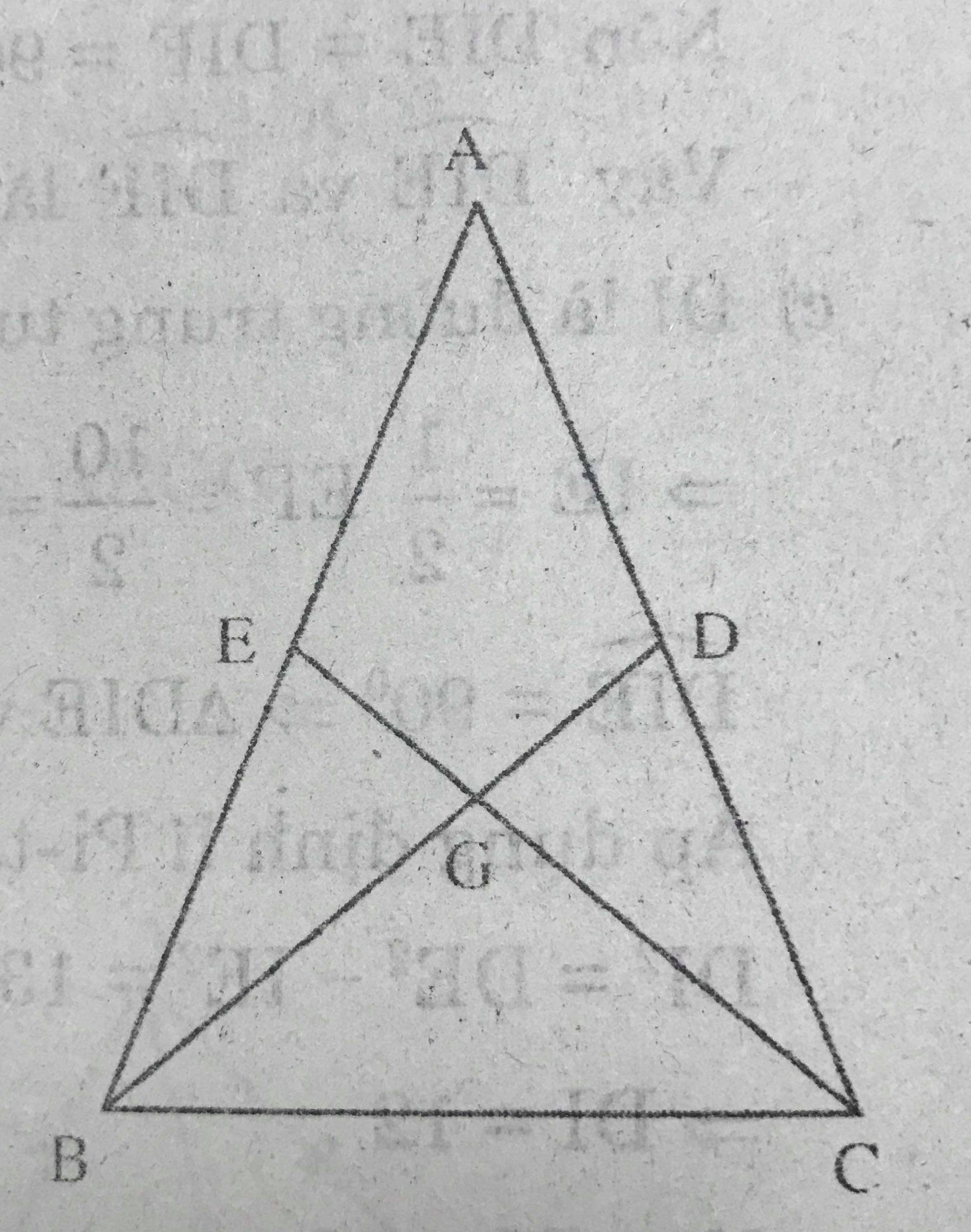
Xét tam giác ABC có trọng tâm G và các đường trung tuyến BD, CE bằng nhau.

Theo tính chất trọng tâm của tam giác , ta có :

GB = \(\dfrac{2}{3}\) BD , GC = \(\dfrac{2}{3}\)CE

Mà BD = CE nên GB = GC => GD = GE

\(\triangle\)BGE và \(\triangle\)CGD có :

GB = GC ; GE = GD

\(\widehat{BGE}=\widehat{CGD}\) (hai góc đỉnh)

Nên \(\triangle\)BGE = \(\triangle\)CGD (c.g.c) => BE = CD

=> \(\dfrac{1}{2}\)AB = \(\dfrac{1}{2}\)AC (BD , CE là các đường trung tuyến của \(\triangle\)ABC)

=> AB = AC => \(\triangle\)ABC cân ở A