Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 4. Tính chất ba đường trung tuyến của tam giác
Đề kiểm tra 15 phút - Đề số 3 - Bài 4 - Chương 3 – Hình học 7
Đề kiểm tra 15 phút - Đề số 3 - Bài 4 - Chương 3 – Hình học 7
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác ABC đường trung tuyến BD. Trên tia đối của tia DB lấy điểm E sao cho \(DE = B{\rm{D}}.\) Gọi M, N theo thứ tự là trung điểm của BC và EC. Gọi P, Q lần lượt là giao điểm của AM, AN với BE. Chứng minh rằng: \(BP = PQ = QE.\)
Hướng dẫn giải
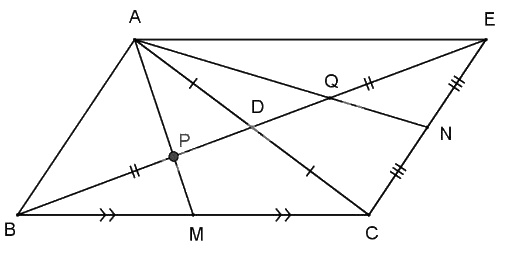
M là trung điểm của BC (gt) nên AM là đường trung tuyến của \(\Delta ABC\).
Lại có BD là trung tuyến của \(\Delta ABC\), mà AM cắt BE tại P nên P là trọng tâm của \(\Delta ABC\), ta có: \(BP = \dfrac{2 }{ 3}B{\rm{D}}.\)
Chứng minh tương tự ta có Q là trọng tâm của \(\Delta AC{\rm{E}} \Rightarrow QE = \dfrac{2 }{ 3}DE\)
mà \(DE = B{\rm{D}}\) (gt) \( \Rightarrow BP = QE.\)
Mặt khác vì \(PB = 2P{\rm{D}}\) (tính chất trọng tâm) và \(QE = 2Q{\rm{D}}\), do đó \(BP = PQ = QE.\)
Copyright © 2021 HOCTAP247
