Trang chủ
Lớp 7
Toán Lớp 7 SGK Cũ
Bài 4. Tính chất ba đường trung tuyến của tam giác
Giải bài 25 trang 67 - Sách giáo khoa Toán 7 tập 2
Giải bài 25 trang 67 - Sách giáo khoa Toán 7 tập 2
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Biết rằng: Trong một tam giác vuông. Đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền. Hãy giải bài toán sau:
Cho tam giác vuông ABC có hai góc vuông AB = 3cm, AC= 4cm. Tính khoảng cách từ đỉnh A tới trọng tâm G của tam giác ABC.
Hướng dẫn giải
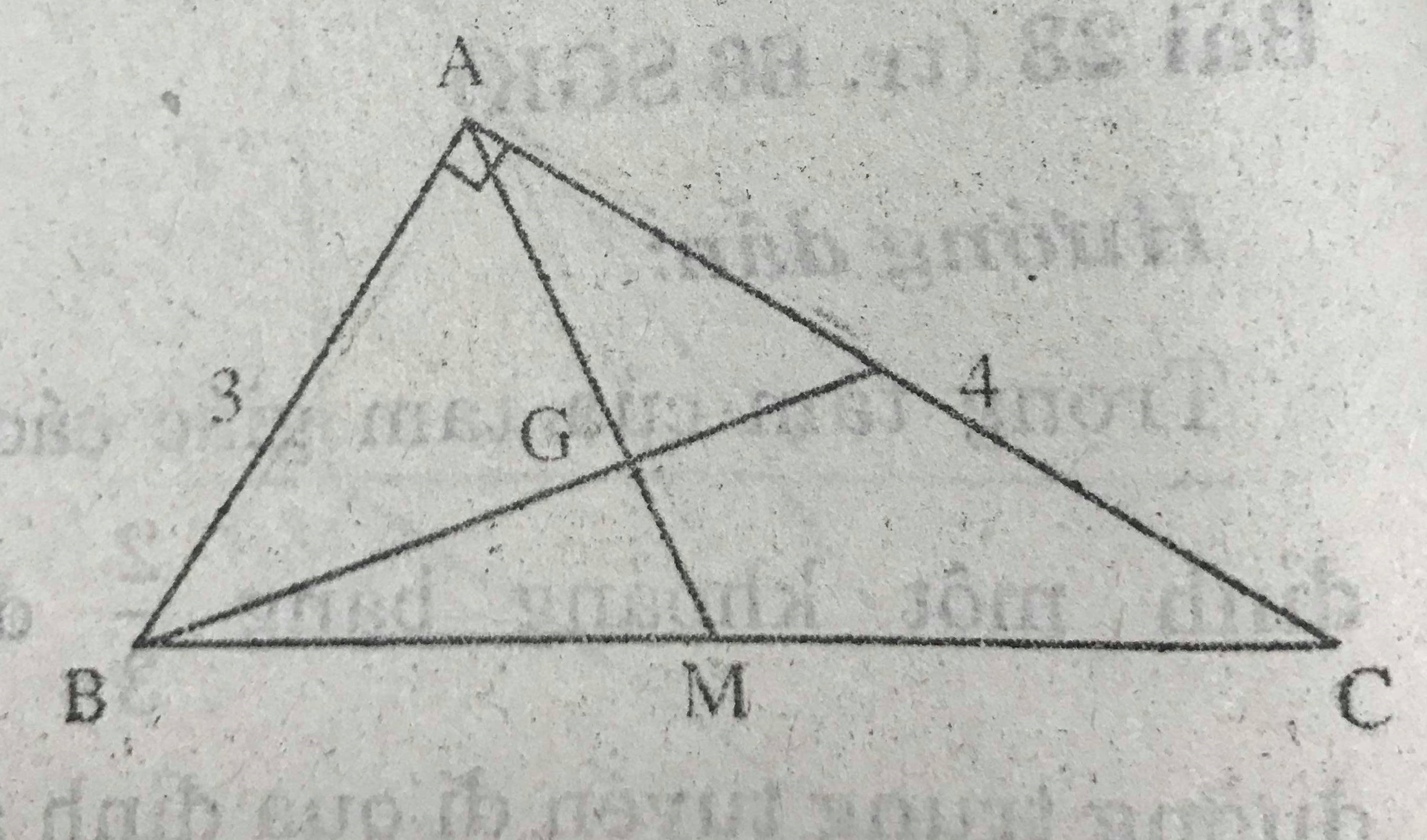
Gọi M là trung điểm của BC.
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC , ta có :
\(BC^2=AB^2+AC^2=3^2+4^2=25=5^2 \Rightarrow BC = 5 (cm)\)
Do đó : AM = \(\dfrac{1}{2}\) BC = \(\dfrac{5}{2}\) (cm)
Theo vị trí trọng tâm, ta có :
AG = \(\dfrac{2}{3}AM=\dfrac{2}{3}.\dfrac{5}{2}=\dfrac{5}{3}\) (cm)
Copyright © 2021 HOCTAP247
