Giải bài 28 trang 67 - Sách giáo khoa Toán 7 tập 2

Đề bài

Cho tam giác DEF cân tại D với đường trung tuyến DI.

a) Chứng minh ΔDEI = ΔDFI.

b) Các góc DIE và góc DIF là những góc gì?

c) Biết DE = DF = 13cm, EF = 10cm, hãy tính độ dài đường trung tuyến DI.

Hướng dẫn giải

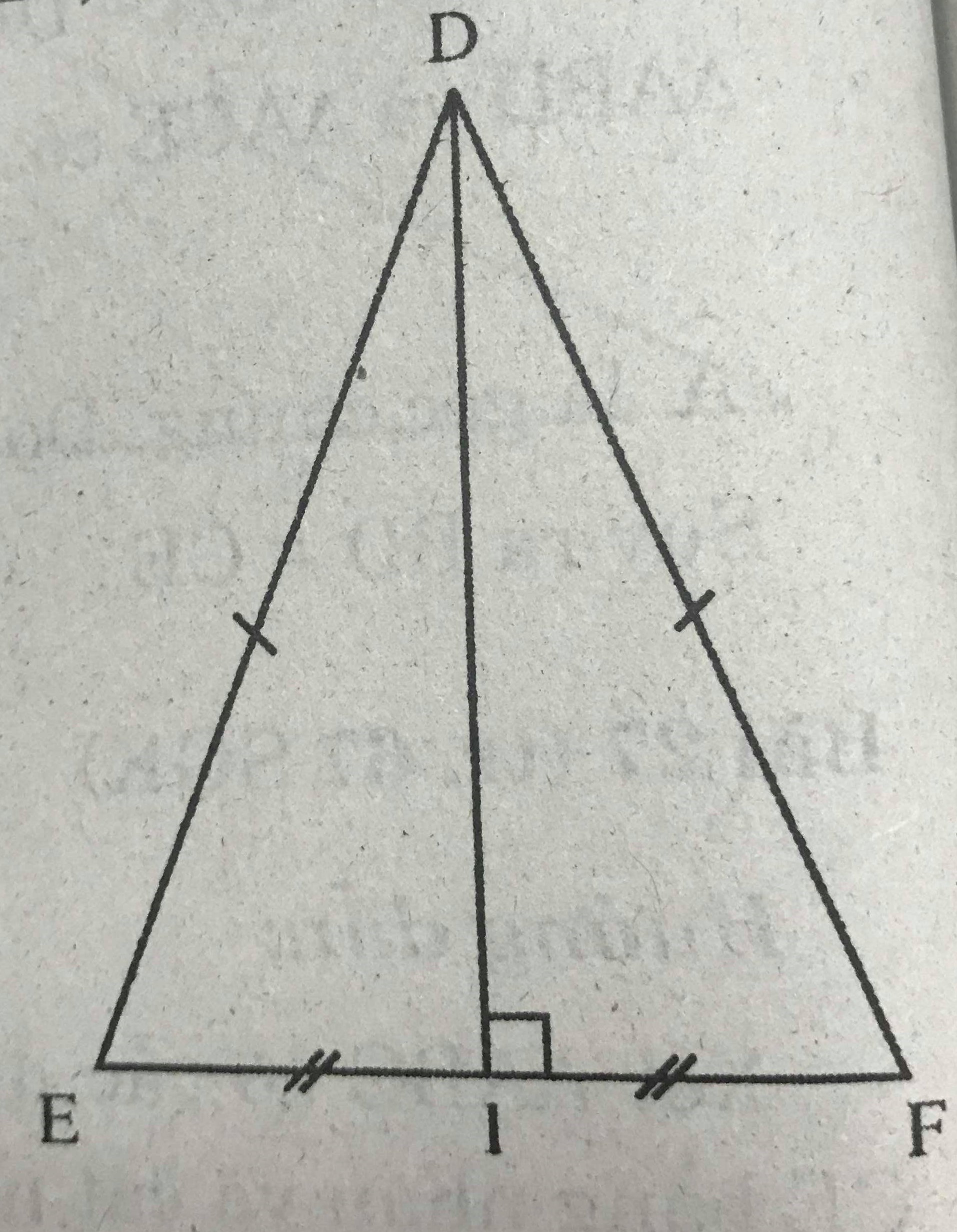
a) ΔDEI và ΔDFI có :

DE = DF (hai cạnh bên của tam giác cân DEF)

IE = IF (DI là đường trung tuyến của tam giác DEF)

DI là cạnh chung

Nên ΔDEI = ΔDFI (c.c.c)

b) ΔDEI = ΔDFI suy ra 

\(\widehat{DIE}+\widehat{DIF}=180^0\)

Nên \(\widehat{DIE}=\widehat{DIF}=90^0\)

Vậy \(\widehat{DIE}\) và \(\widehat{DIF}\) là các góc vuông.

c) DI là đường trung tuyến của ΔDEF

=> IE = \(\dfrac{1}{2}\)EF = \(\dfrac{10}{2}\) = 5 (cm)

\(\widehat{DIE}=90^0 \Rightarrow\) ΔDIE vuông tại I

Áp dụng định lí Pi-ta-go vào tam giác vuông DIE, ta có :

\(DI^2=DE^2-IE^2=13^2-5^2=169-25=144=12^2\)

=> DI = 12

Vậy DI = 12cm