Bài 23 trang 123 SGK Toán 8 tập 1

Đề bài

Cho tam giác \(ABC\). Hãy chỉ ra một số vị trí của điểm \(M\) nằm trong tam giác đó sao cho:

                     \({S_{MAC}} = {S_{MAB}} + {S_{BMC}}\)

Hướng dẫn giải

- Kẻ đường cao \(BH, MK.\)

- Áp dụng công thức tính diện tích tam giác.

Lời giải chi tiết

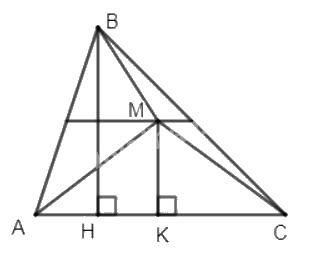
Kẻ đường cao \(BH, MK.\)

Theo giả thiết, \(M\) là điểm nằm trong tam giác \(ABC\) sao cho:

\({S_{AMB}} + {\rm{ }}{S_{BMC}} = {\rm{ }}{S_{MAC}}\)

Ta lại có: \({S_{AMB}} + {S_{BMC}} + {S_{MAC}} = {S_{ABC}}\)

Suy ra: \({S_{MAC}}+ {S_{MAC}}={S_{ABC}}\)

Hay \({S_{MAC}} = {1 \over 2}{S_{ABC}}\)

\(\Rightarrow {1 \over 2}MK.AC = {1 \over 2}\left( {{1 \over 2}BH.AC} \right)\)

\(⇒ MK = {1 \over 2}BH\)

Do đó, \(M\) nằm trên đường thẳng sao cho khoảng cách từ \(M\) đến \(AC\) bằng \( {1 \over 2}\) đường cao \(BH\).

Vậy điểm \(M\) nằm trên đường trung bình ứng với cạnh \(AC\) của \(ΔABC\)