Trang chủ
Lớp 8
Toán Lớp 8 SGK Cũ
Bài 3. Diện tích tam giác
Giải bài 24 trang 123 - Sách giáo khoa Toán 8 tập 1
Giải bài 24 trang 123 - Sách giáo khoa Toán 8 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Tính diện tích của một tam giác cân có cạnh đáy bằng a và cạnh bên bằng b.
Hướng dẫn giải
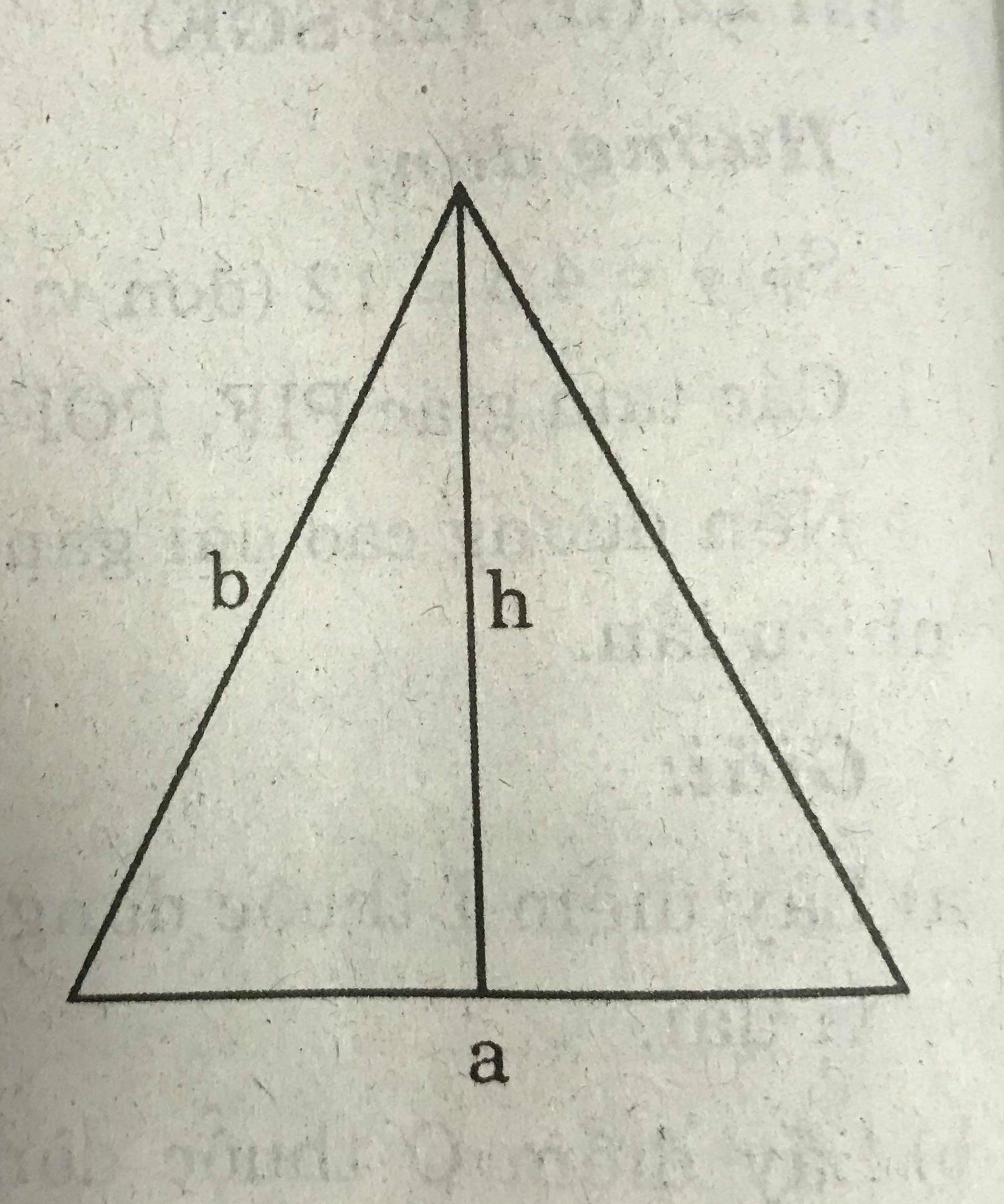
Gọi h là chiều cao của tam giác cân có đáy là a và cạnh bên là b.
Theo định lí Pi-ta-go , ta có :
\(h^2=b^2-(\dfrac{a}{2})^2=\dfrac{4b^2-a^2}{4}\)
=> \(h = \dfrac{\sqrt{4b^2-a^2}}{2}\)
Vậy , S = \(\dfrac{1}{2}ah\) = \(\dfrac{1}{2}a\dfrac{\sqrt{4b^2-a^2}}{2}\)
= \(\dfrac{1}{4}a\sqrt{4b^2-a^2}\) (đvđt)
Copyright © 2021 HOCTAP247
