Trang chủ
Lớp 8
Toán Lớp 8 SGK Cũ
Bài 3. Diện tích tam giác
Giải bài 23 trang 123 - Sách giáo khoa Toán 8 tập 1
Giải bài 23 trang 123 - Sách giáo khoa Toán 8 tập 1
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Cho tam giác ABC. Hãy chỉ ra một số vị trí của điểm M nằm trong tam giác đó sao cho: S\(_{AMB}\) + S\(_{BMC}\) = S\(_{MAC}\)
Hướng dẫn giải
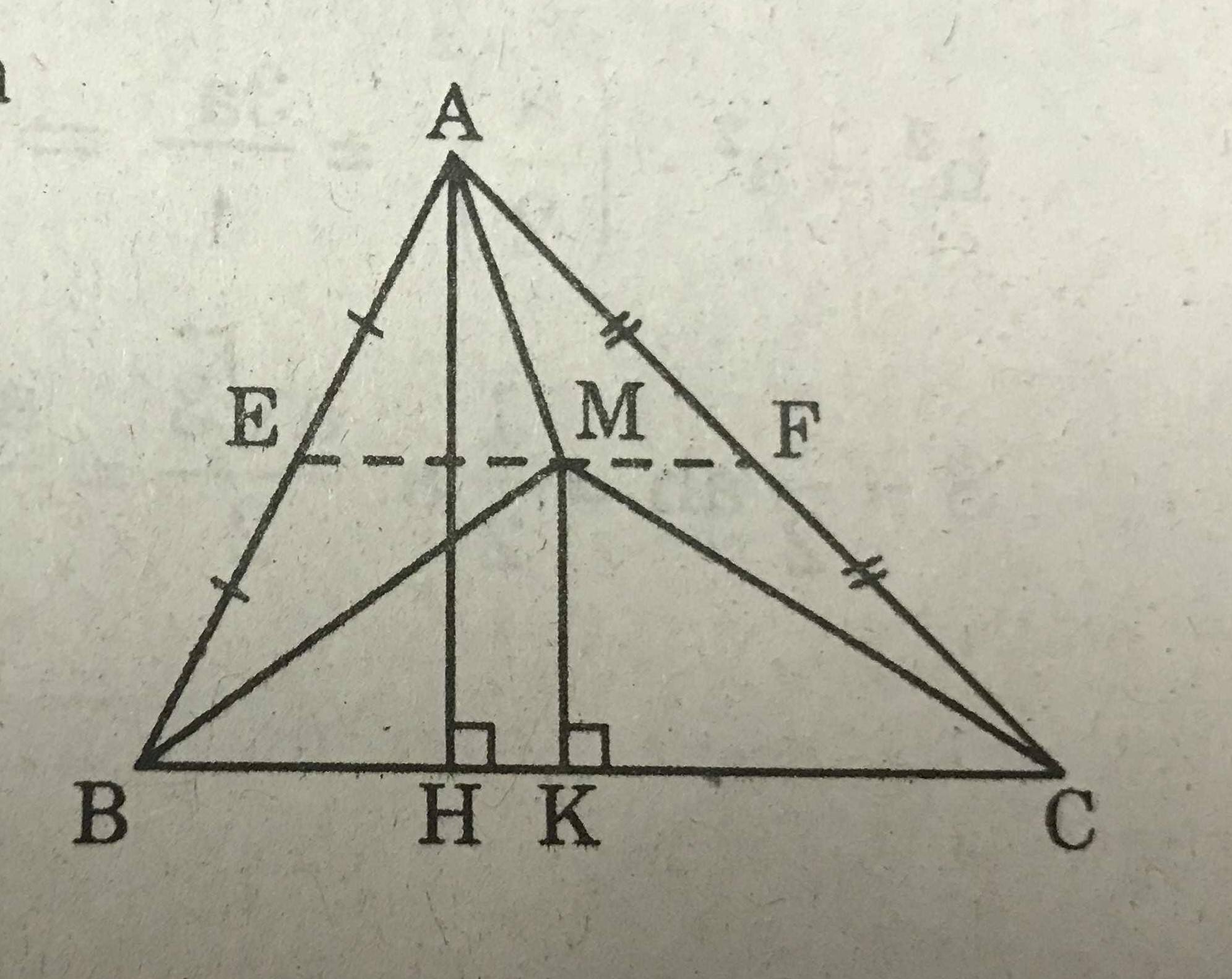
Theo giả thiết thì M là điểm nằm trong tam giác ABC sao cho :
S\(_{AMB}\) + S\(_{BMC}\) = S\(_{MAC}\)
Nhưng S\(_{AMB}\) + S\(_{BMC}\) + S\(_{MAC}\) = S\(_{ABC}\)
Nên S\(_{MAC}\) = \(\dfrac{1}{2}\)S\(_{ABC}\)
\(\triangle\)MAC và \(\triangle\)ABC có chung đáy BC nên MK = \(\dfrac{1}{2}\)BH
Vậy, điểm M nằm trên đường trung bình EF của \(\triangle\)ABC.
Copyright © 2021 HOCTAP247
