Giải bài 20 trang 122 - Sách giáo khoa Toán 8 tập 1
Tóm tắt bài
Đề bài
Vẽ hình chữ nhật có một cạnh bằng cạnh của một tam giác cho trước và có diện tích bằng diện tích của tam giác đó. Từ đó suy ra một cách chứng minh khác về công thức tính diện tích tam giác.
Hướng dẫn giải
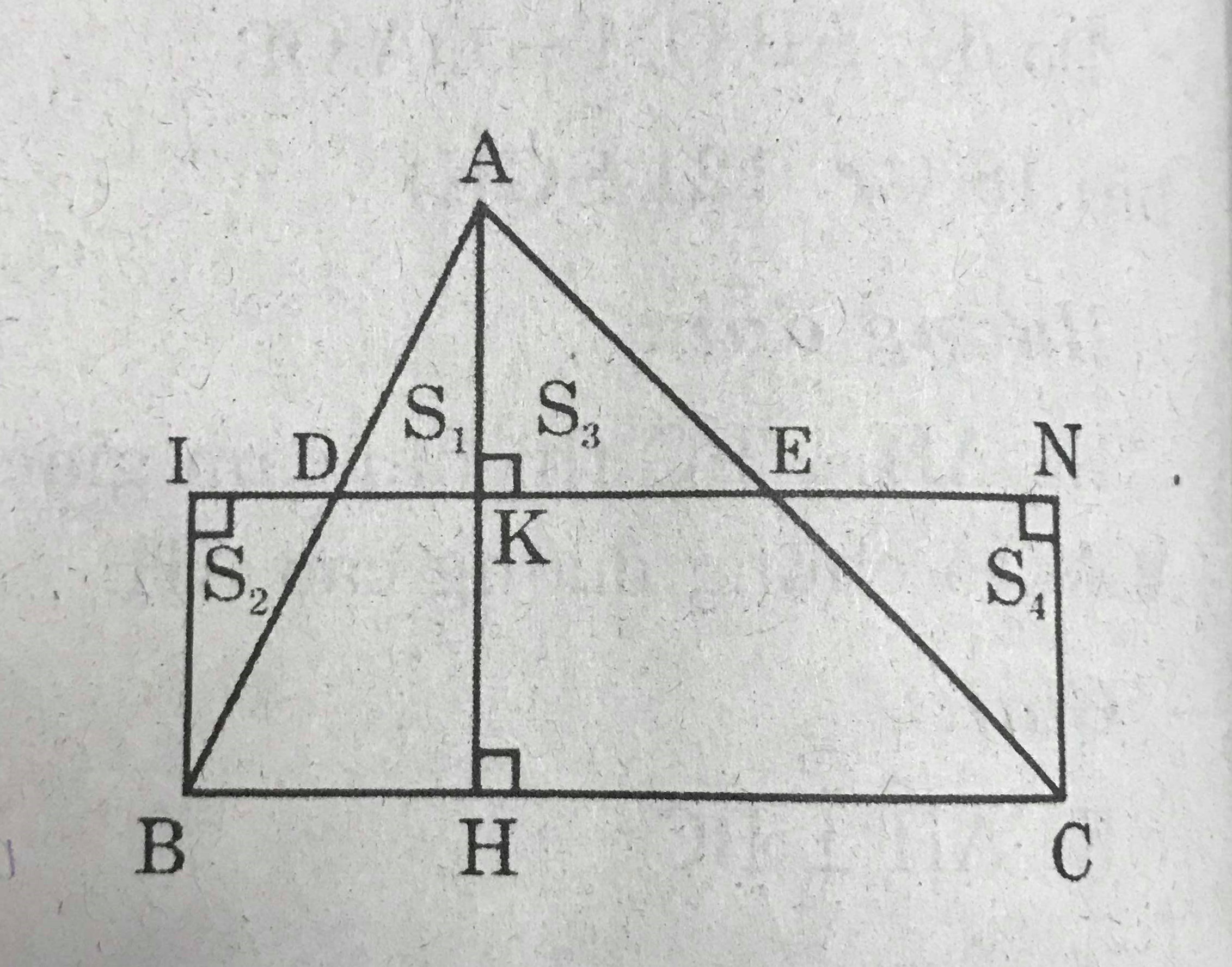
Dựng hình chữ nhật có một cạnh là cạnh của tam giác, cạnh đối diện thuộc đường thẳng đi qua trung điểm hai cạnh kia.
Kẻ AK \(\perp\) DE (nếu chọn BC là cạnh lớn nhất của \(\triangle\)ABC thì AK không nằm ngoài tam giác)
Xét hai tam giác vuông \(\triangle\)BID và \(\triangle\)AKD có :
\(\widehat{BDI}=\widehat{ADK}\) (đối đỉnh) , DA = DB
Nên \(\triangle\)BID = \(\triangle\)AKD (cạnh huyền - góc nhọn) => S\(_1\) = S\(_2\)
Tương tự : S\(_3\) = S\(_4\)
Do đó : \(S_{ABC}=S_{BNC}\)
Suy ra : \(S_{ABC}=S_{BNC}= BC.KH = \dfrac{1}{2}BC.AH\)
Điều này cho ta một cách chứng minh công thức diện tích tam giác.
Copyright © 2021 HOCTAP247
