Bài 1 trang 68 SGK Toán 9 tập 1

Đề bài

Hãy tính \(x\) và \(y\) trong mỗi hình sau (hình \(4a,\ b)\):

Hướng dẫn giải

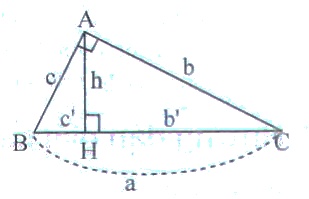
+) Sử dụng định lí Pytago trong tam giác vuông: \(\Delta{ABC}\) vuông tại \(A\), khi đó: \(BC^2=AC^2+AB^2\).

+) Sử dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền:

  \(b^2=a.b',\ c^2=a.c'\)

Lời giải chi tiết

a) Đặt tên các đỉnh của tam giác như hình dưới:

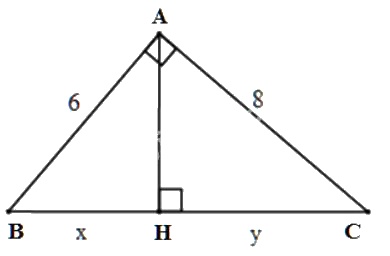
 Áp dụng định lí Pytago vào \(\Delta{ABC}\) vuông tại \(A\), ta có:

\(BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10\)

 Áp dụng hệ thức lượng vào\(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có:

\(AB^2=BC.BH\Rightarrow BH=\dfrac{AB^2}{BC}=\dfrac{6^2}{10}=3,6\)

Lại có \(HC=BC-BH=10-3,6=6,4\)

Vậy \(x =BH= 3,6\);  \(y=HC = 6,4\).

b) Đặt tên các đỉnh của tam giác như hình dưới

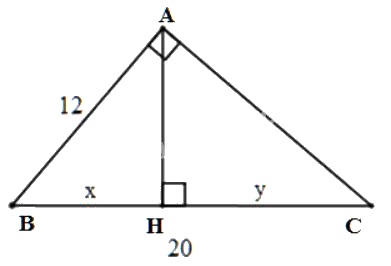
Áp dụng hệ thức lượng vào \(\Delta{ABC}\) vuông tại \(A\), đường cao \(AH\), ta có:

\(AB^2=BH.BC  \Leftrightarrow 12^2=20.x \Rightarrow x=\dfrac{12^2}{20}=7,2\)

Lại có: \(HC=BC-BH=20-7,2=12,8\)

Vậy \(x=BH = 7,2;\)  \(y=HC = 12,8\).