Giải bài 5 trang 69 - Sách giáo khoa Toán 9 tập 1

Đề bài

      Trong tam giác vuông với các cạnh góc vuông có độ dài 3 và 4, kẻ đường cao ứng với cạnh huyền. Hãy tính đường cao này và độ dài các đoạn thẳng mà nó định ra trên cạnh huyền.

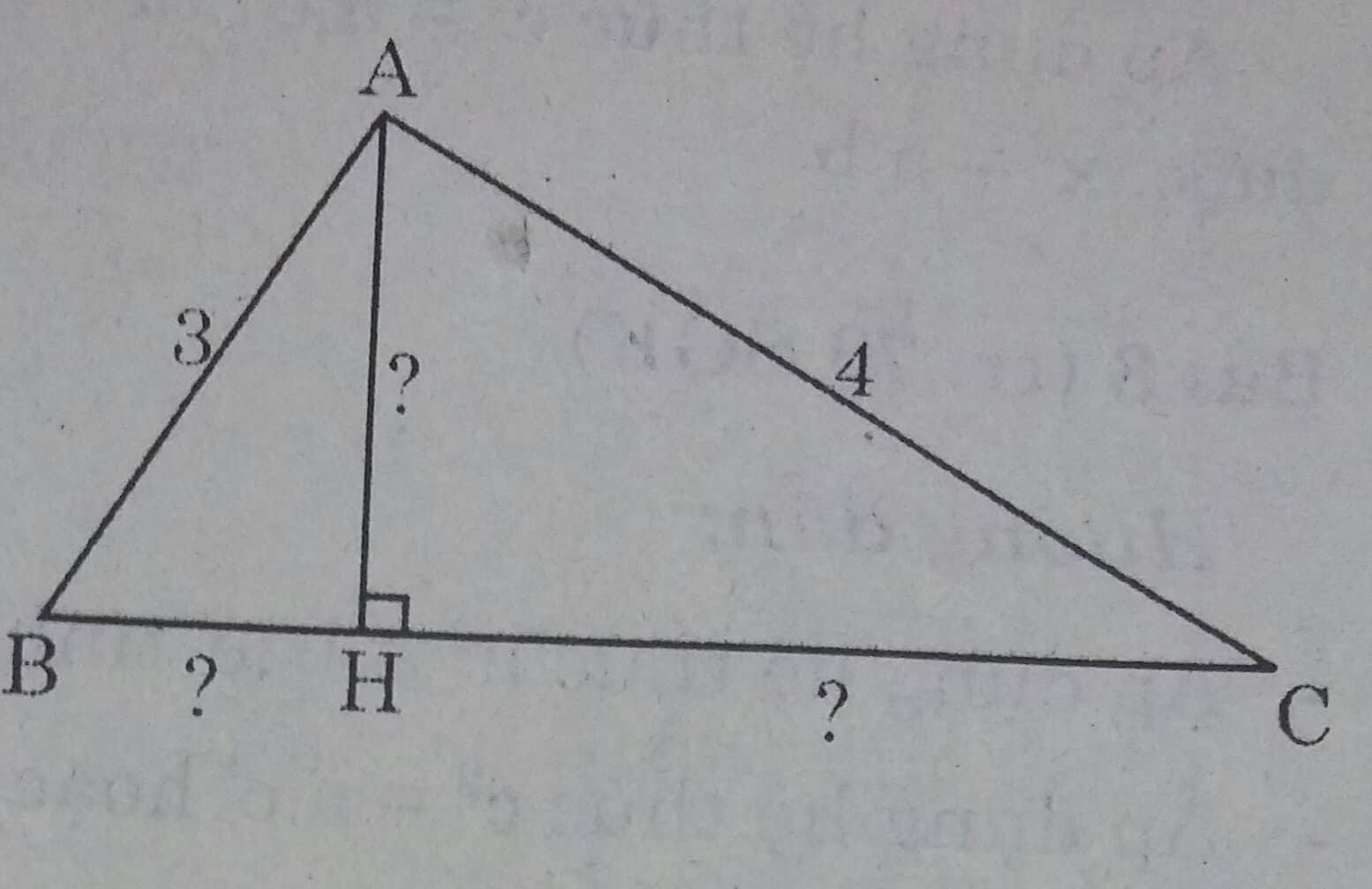
Hướng dẫn giải

     Hướng dẫn:

- Áp dụng định lý Py-ta-go để tính được độ dài BC.

- Áp dụng hệ thức \(c^2=a.c'\) để tính được độ dài HB. 

- Áp dụng hệ thức \(b^2=a.b'\) để tính được độ dài HC. 

- Áp dụng hệ thức \(h^2=b'.c'\) để tính được độ dài AH. 

   Giải: 

   Áp dụng định lí Py-ta-go ta có: 

 \( BC= \sqrt{AB^2+AC^2}= \sqrt{3^2+4^2}=5\)

 Áp dụng hệ thức \(c^2=a.c'\) ta được: 

   \(3^2= 5.HB \Rightarrow HB= 1,8\)

 Áp dụng hệ thức \(b^2=a.b'\) ta được: \(4^2= 5.HB \Rightarrow HC=3,2\) 

 Áp dụng hệ thức \(h^2=b'.c'\) ta được: \(AH= \sqrt{1,8.3,2}=2,4\)