Đề kiểm tra 15 phút - Đề số 1 - Bài 1 - Chương 1 - Hình học 9
Tóm tắt bài
Đề bài
Cho ∆ABC vuông tại A có \(AB = 30cm\), đường cao \(AH = 24cm\).
a. Tính BH, BC, AC.
b. Đường thẳng vuông góc với AB tại B cắt tia AH tại B. Tính BD.
Hướng dẫn giải
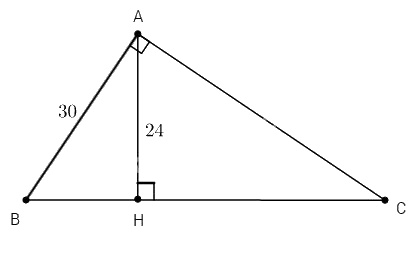
a. Ta có: ∆AHB vuông tại H. Theo định lí Pi-ta-go :
\(\eqalign{ & B{H^2} = A{B^2} - A{H^2} \cr & \Rightarrow BH = \sqrt {A{B^2} - A{H^2}} \cr&\;\;\;\;\;\;\;\;\;\;\;\;= \sqrt {{{30}^2} - {{24}^2}} = 18\,\left( {cm} \right) \cr} \)
Lại có ∆ABC vuông tại A
\(A{B^2} = BC.BH\) (định lí 1)
\( \Rightarrow BC = {{A{B^2}} \over {BH}}\)\(\; = {{{{30}^2}} \over {18}} = 50\,cm\)
Do đó \(A{C^2} = B{C^2} - A{B^2}\) (định lí Pi-ta-go)
\( \Rightarrow AC = \sqrt {B{C^2} - A{B^2}} \)\(\;= \sqrt {{{50}^2} - {{30}^2}} = 40\,\left( {cm} \right)\)
b. Ta có: ∆ABD vuông tại B, đường cao là BH nên:
\(A{B^2} = AD.AH\) (định lí 1)
\( \Rightarrow AD = {{A{B^2}} \over {AH}} = {{{{30}^2}} \over {24}} = 37,5\,\left( {cm} \right)\)
Do đó \(HD = AD - AH = 37,5 - 24 \)\(\;= 13,5\,\left( {cm} \right)\)
\( \Rightarrow B{D^2} = AD.HD\) (định lí 1)
\( \Rightarrow BD = \sqrt {AD.HD} = \sqrt {37,5.13,5} \)\(\;= 22,5\,\left( {cm} \right)\)
Copyright © 2021 HOCTAP247
