Trang chủ
Lớp 9
Toán Lớp 9 SGK Cũ
Bài 10. Diện tích hình tròn, hình quạt tròn
Đề kiểm 15 phút - Đề số 2 - Bài 10 - Chương 3 - Hình học 9
Đề kiểm 15 phút - Đề số 2 - Bài 10 - Chương 3 - Hình học 9
Lý thuyết
Bài tập
Mục lục
Tóm tắt bài
Đề bài
Tính theo a diện tích hình tròn (O).
a) Biết độ dài cạnh của hình vuông nội tiếp đường tròn (O) là a.
b) Biết độ dài cạnh của tam giác đều nội tiếp của đường tròn (O) là a.
Hướng dẫn giải
a)
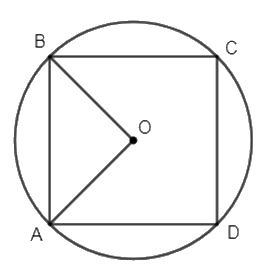
Ta có :\(AB = R\sqrt 2 \) ( cạnh hình vuông nội tiếp (O; R)) hay \(a = R\sqrt 2 \Rightarrow R = \dfrac{a}{{\sqrt 2 }}\)
Do đó \(S_{\text{ hình tròn}}=\pi {R^2} = \dfrac{{\pi {a^2}}}{2}\) (đvdt)
b)
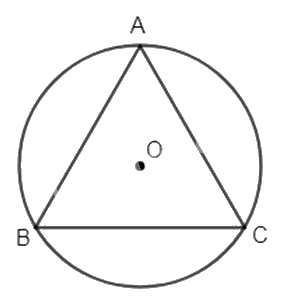
\(AB = R\sqrt 3 \) (cạnh của tam giác đều nội tiếp (O; R)) hay \(a = R\sqrt 3 \Rightarrow R = \dfrac{a}{{\sqrt 3 }}\) .
Do đó \(S_{\text{hình tròn}}=\pi {R^2} = \pi {\left( {\dfrac{a}{{\sqrt 3 }}} \right)^2} = \dfrac{{\pi {a^2}}}{3}\)(đvdt).
Copyright © 2021 HOCTAP247
