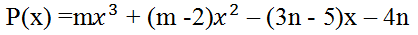Giải bài 19 trang 16 - Sách giáo khoa Toán 9 tập 2

Đề bài

    Biết rằng: Đa thức P(x) chia hết cho đa thức x – a khi và chỉ khi P(a) = 0. Hãy tìm các giá trị của m và n sao cho đa thức sau đồng thời chia hết cho x + 1 và x – 3:

Hướng dẫn giải

    P(x) chia hết cho  x+ 1 \(\Rightarrow\) P(-1)= -m + (m-2)+ (3n - 5) - 4n = 0 

   \( \Leftrightarrow - 7 -n = 0 \) (1)

  P(x) chia hết cho x- 3  \(\Leftrightarrow\) P(3) = 27m + 9( m-2) - 3(3n -5) - 4n = 0

  \(\Leftrightarrow 36m - 13n = 13\) ( 2) 

   Từ (1) và (2) ta có hệ phương trình ẩn m và n:

   \(\left\{\begin{matrix} & - 7-n = 0\\ & 36m - 13n = 3\end{matrix}\right. \Leftrightarrow \)\(\left\{\begin{matrix} & n = ​​-7\\ & m =- \dfrac{22}{9}\end{matrix}\right. \)

 Vậy với \(m =- \dfrac{22}{9}\) và n = -7 thì đa thức P(x) đồng thời chia hết cho x+1 và x- 3