Bài 15 trang 75 SGK Toán 8 tập 1
Tóm tắt bài
Đề bài
Cho \(\Delta ABC\) cân tại A. Trên các cạnh bên AB, AC lấy theo thứ tự các điểm D và E sao cho AD = AE.
a) Chứng minh rằng BDEC là hình thang cân.
b) Tính các góc của hình thang cân đó, biết rằng \(\widehat{A}\)=500
Hướng dẫn giải
- Áp dụng: dấu hiệu nhận biết hình thang cân, định lý tổng ba góc trong tam giác, tính chất tam giác cân, tính chất hình thang cân.
Lời giải chi tiết
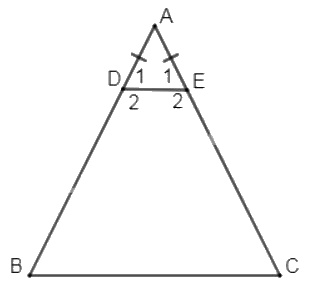
a) Ta có AD = AE (gt) nên ∆ADE cân (dấu hiệu nhận biết tam giác cân)
\( \Rightarrow \widehat{D_{1}}\) = \(\widehat{E_{1}}\) (tính chất tam giác cân)
Xét ∆ADE có: \(\widehat {{D_1}} + \widehat {{E_1}} + \widehat A = {180^0}\) (định lý tổng ba góc trong tam giác)
\(\begin{array}{l}
\Rightarrow 2\widehat {{D_1}} + \widehat A = {180^0}\\
\Rightarrow \widehat {{D_1}} = \frac{{{{180}^0} - \widehat A}}{2}\left( 1 \right)
\end{array}\)
Vì ∆ABC cân tại A (gt) \(\Rightarrow \widehat B = \widehat C\) (tính chất tam giác cân)
Mà: \(\widehat A + \widehat B + \widehat C = {180^0}\) (định lý tổng ba góc trong tam giác)
\(\begin{array}{l}
\Rightarrow \widehat {2B} + \widehat A = {180^0}\\
\Rightarrow \widehat B = \frac{{{{180}^0} - \widehat A}}{2}\left( 2 \right)
\end{array}\)
Từ (1) và (2) \(\Rightarrow \widehat{D_{1}}\) = \(\widehat{B}\), mà hai góc này là hai góc đồng vị nên suy ra DE // BC (dấu hiệu nhận biết hai đường thẳng song song)
Do đó BDEC là hình thang (dấu hiệu nhận biết hình thang).
Lại có \(\widehat{B}\) = \(\widehat{C}\) ( cmt )
Nên BDEC là hình thang cân (dấu hiệu nhận biết hình thang cân).
b) Với \(\widehat{A}\)=500
Ta được \(\widehat{B}\) = \(\widehat{C}\) = \(\frac{180^{0}-\widehat{A}}{2}\) = \(\frac{180^{0}-50^{0}}{2}\) = 650
\(\widehat {{D_2}} + \widehat B = {180^0}\) (2 góc trong cùng phía bù nhau)
\(\Rightarrow \widehat {{D_2}} = {180^0} - \widehat B = {180^0} - {65^0} \)\(= {115^0}\)
Mà BDEC là hình thang cân (cmt)\(\Rightarrow \widehat {{D_2}} = \widehat {{E_2}}= {115^0}\) (tính chất hình thang cân)
Copyright © 2021 HOCTAP247
