Giải bài 18 trang 75 - Sách giáo khoa Toán 8 tập 1

Đề bài

Chứng minh định lý: "Hình thang có hai đường chéo bằng nhau là hình thang cân" qua bài toán sau: Cho hình thang ABCD (AB // CD) có AC = BD. Qua B kẻ đường thẳng song song với AC, cắt đường thẳng DC tại tại E. Chứng minh rằng:

a) ΔBDE là tam giác cân.

b) ΔACD = ΔBDC

c) Hình thang ABCD là hình thang cân.

Hướng dẫn giải

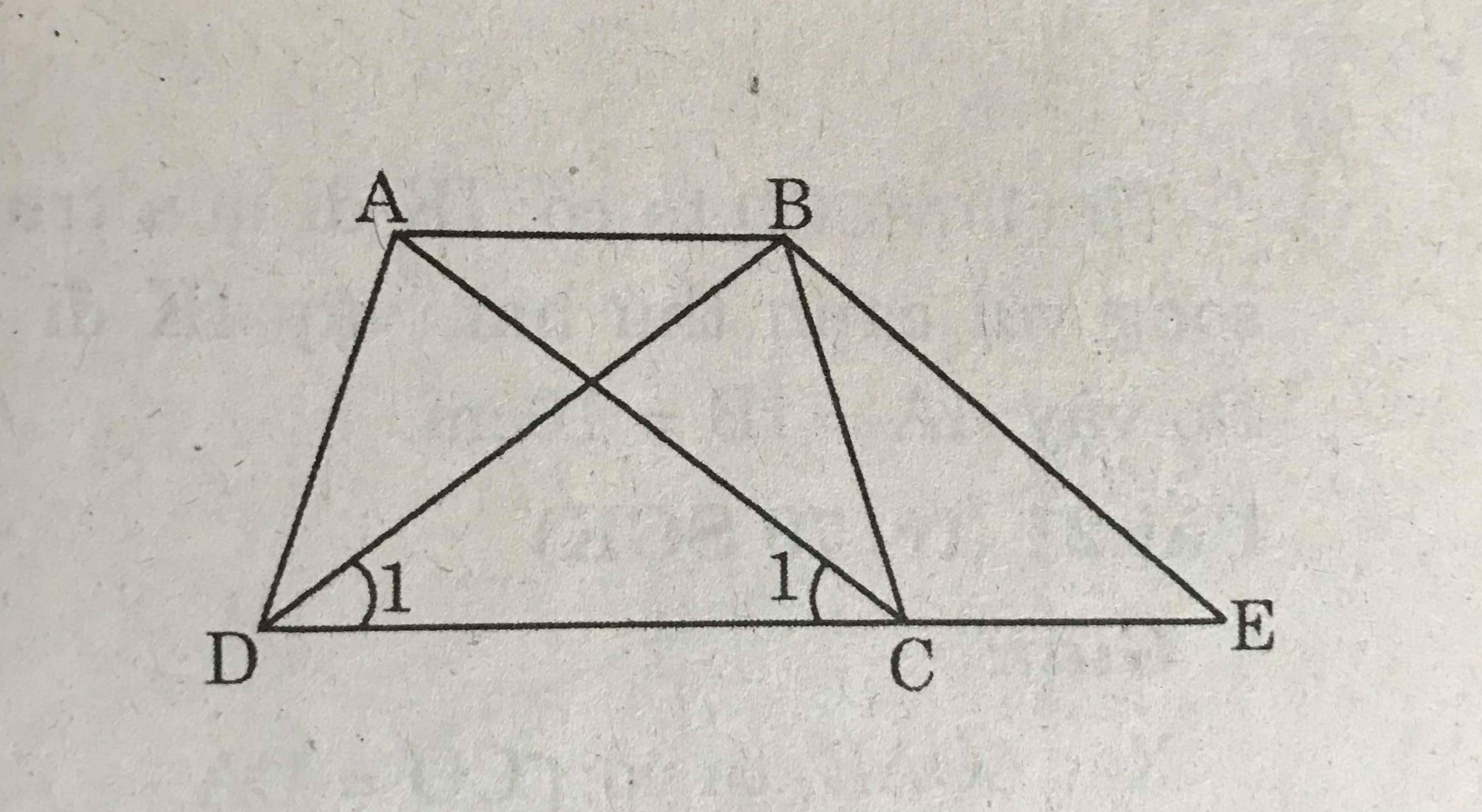
a) AB // CE (AB, EC là hai đáy của hình thang)

AC // BE (gt)

Nên AC = BE.

Mặt khác AC = BD (gt) suy ra BE = BD

Do đó : ΔBDE cân.

b) AC // BE => \(\widehat{C_1}=\widehat{E}\)

ΔBDE cân tại B (câu a)

=> \(\widehat{D_1}=\widehat{E}\)

Suy ra : \(\widehat{C_1}=\widehat{D_1}\)

=> ΔACD = ΔBDC (c.g.c)

c) ΔACD = ΔBDC => \(\widehat{ADC}=\widehat{BCD}\)

Suy ra : ABCD là hình thang cân.