Giải bài 16 trang 75 - Sách giáo khoa Toán 8 tập 1

Đề bài

Cho tam giác ABC cân tại A, các đường phân giác BD, CE (D ∈ AC, E ∈ AB). Chứng minh rằng BEDC là hình thang cân có đáy nhỏ bằng cạnh bên.

Hướng dẫn giải

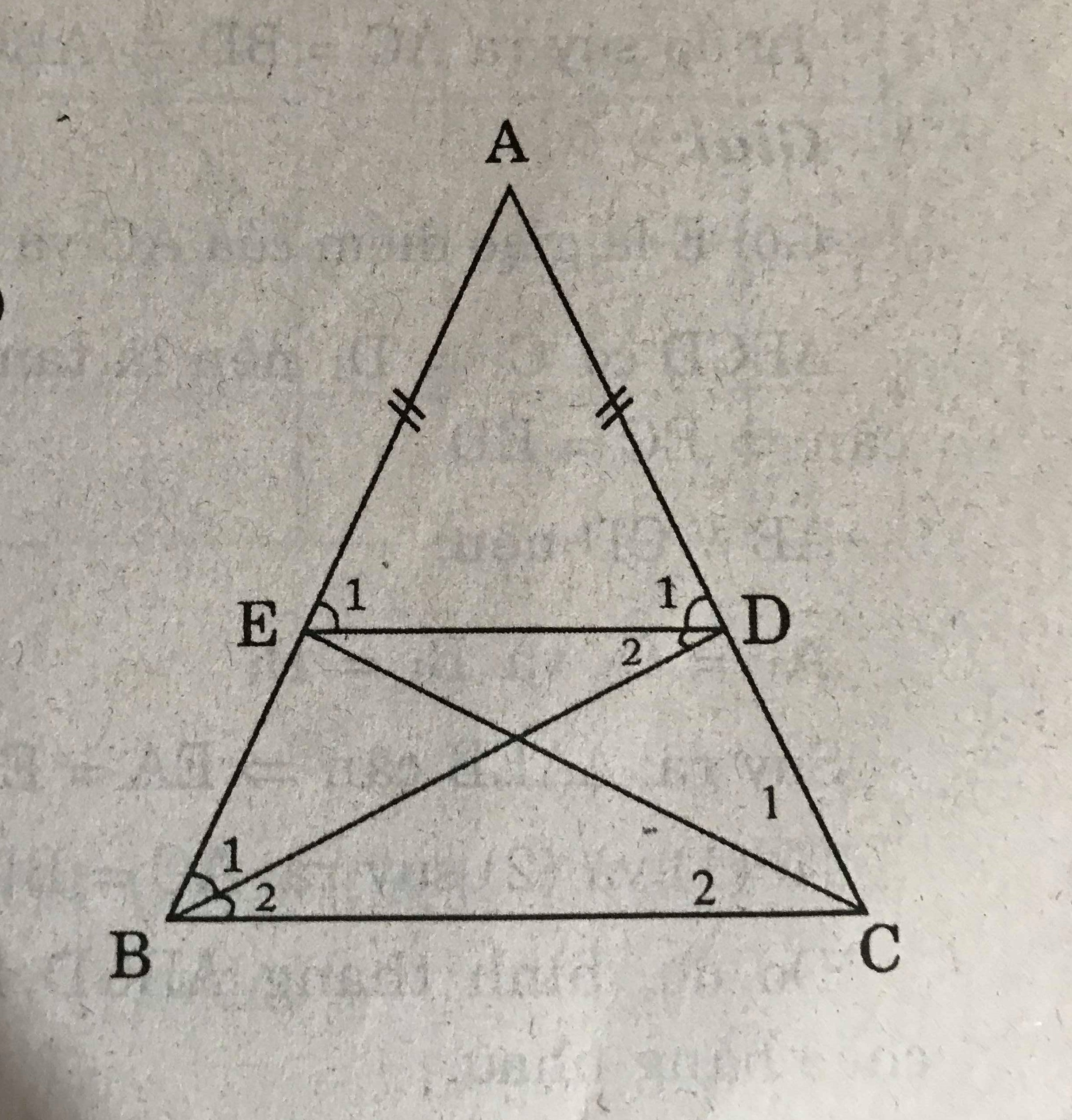
Xét \(\triangle\)ABD và \(\triangle\)ACE , ta có :

\(\widehat{A}\) chung; AB = AC ( \(\triangle\)ABC cân)

\(\widehat{B_1}=\widehat{C_1}\) (BD, CE là hai tia phân giác của hai góc đáy trong tam giác cân)

Nên \(\triangle\)ABD = \(\triangle\)ACE => AD = AE

=> \(\triangle\)ADE cân => \(\widehat{D_1}=\widehat{E_1}\)

\(\triangle\)ABC cân => \(\widehat{C}=\dfrac{180^0-\widehat{A}}{2}\)

Nên \(\widehat{D_1}=\widehat{C} \Rightarrow DE //BC \Rightarrow\) BEDC là hình thang.

Lại có : \(\widehat{B}=\widehat{C}\) nên BEDC là hình thang cân

Cũng vì DE // BC nên \(\widehat{D_1}=\widehat{B_2}\) (so le trong)

Mặt khác \(\widehat{B_1}=\widehat{B_2}\) suy ra \(\widehat{B_1}=\widehat{D_2}\)

Do đó : DE = BE