Rút gọn phân số
Tóm tắt bài
1.1. Kiến thức cần nhớ
a) Cho phân số \(\frac{{10}}{{15}}\). Tìm phân số bằng phân số \(\frac{{10}}{{15}}\) nhưng có tử số và mẫu số bé hơn.
Ta có thể làm như sau :
Ta thấy 10 và 15 đều chia hết cho 5. Theo tính chất cơ bản của phân số ta có :
\(\frac{{10}}{{15}} = \frac{{10:5}}{{15:5}} = \frac{2}{3}\)
Vậy : \(\frac{{10}}{{15}} = \frac{2}{3}\).
Nhận xét :
- Tử số và mẫu số của phân số \(\frac{2}{3}\) đều bé hơn tử số và mẫu số của phân số \(\frac{{10}}{{15}}\).
- Hai phân số \(\frac{2}{3}\) và \(\frac{{10}}{{15}}\) bằng nhau.
Ta nói rằng : Phân số \(\frac{{10}}{{15}}\) đã được rút gọn thành phân số \(\frac{2}{3}\).
Có thể rút gọn phân số để được một phân số có tử số và mẫu số bé đi mà phân số mới vẫn bằng phân số đã cho.
b) Cách rút gọn phân số
Ví dụ 1: Rút gọn phân số \(\frac{6}{8}\).
Ta thấy : 6 và 8 đều chia hết cho 2, nên :
\(\frac{6}{8} = \frac{{6:2}}{{8:2}} = \frac{3}{4}\)
3 và 4 đều không cùng chia hết cho một số tự nhiên nào lớn hơn 1, nên phân số \(\frac{3}{4}\) không thể rút gọn được nữa. Ta nói rằng : phân số \(\frac{3}{4}\) là phân số tối giản và phân số \(\frac{6}{8}\) đã được rút gọn thành phân số tối giản \(\frac{3}{4}\).
Ví dụ 2: Rút gọn phân số \(\frac{{18}}{{54}}\).
Ta thấy : 18 và 54 đều chia hết cho 2, nên
\(\frac{{18}}{{54}} = \frac{{18:2}}{{54:2}} = \frac{9}{{27}}\)
9 và 27 đều chia hết cho 9, nên :
\(\frac{9}{{27}} = \frac{{9:9}}{{27:9}} = \frac{1}{3}\)
1 và 3 đều không cùng chia hết cho số tự nhiên nào lớn hơn 1, nên 3434 là phân số tối giản.
Vậy : \(\frac{{18}}{{54}} = \frac{1}{3}\).
Khi rút gọn phân số có thể làm như sau :
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản.
1.2. Giải bài tập Sách giáo khoa trang 114
Bài 1: Rút gọn các phân số
a) \(\frac{4}{6};\frac{{12}}{8} & ;\frac{{15}}{{25}};\frac{{11}}{{22}};\frac{{36}}{{10}};\frac{{75}}{{36}}\)
b) \(\frac{5}{{10}};\frac{{12}}{{36}};\frac{9}{{72}};\frac{{75}}{{300}};\frac{{15}}{{35}};\frac{4}{{100}}\)
Hướng dẫn giải:
Cách rút gọn phân số :
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
a)
\(\begin{array}{l}
\frac{4}{6} = \frac{{4:2}}{{6:2}} = \frac{2}{3}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{12}}{8} = \frac{{12:4}}{{8:4}} = \frac{3}{2}\\
\frac{{15}}{{25}} = \frac{{15:5}}{{25:5}} = \frac{3}{5}\,\,\,\,\,\,\,\,\,\,\,\,\frac{{11}}{{22}} = \frac{{11:11}}{{22:11}} = \frac{1}{2}\\
\frac{{36}}{{10}} = \frac{{36:2}}{{10:2}} = \frac{{18}}{5}\,\,\,\,\,\,\,\,\,\frac{{75}}{{36}} = \frac{{75:3}}{{36:3}} = \frac{{25}}{{12}}
\end{array}\)
b)
\(\begin{array}{l}
\frac{5}{{10}} = \frac{{5:5}}{{10:5}} = \frac{1}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{12}}{{36}} = \frac{{12:12}}{{36:12}} = \frac{1}{3}\\
\frac{9}{{72}} = \frac{{9:9}}{{72:9}} = \frac{1}{8}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{75}}{{300}} = \frac{{75:25}}{{300:25}} = \frac{3}{{12}} = \frac{{3:3}}{{12:3}} = \frac{1}{4}\\
\frac{{15}}{{35}} = \frac{{15:5}}{{35:5}} = \frac{3}{7}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{4}{{100}} = \frac{{4:4}}{{100:4}} = \frac{1}{{25}}
\end{array}\)
Bài 2: Trong các phân số : \(\frac{1}{3};\frac{4}{7};\frac{8}{{12}};\frac{{30}}{{36}};\frac{{72}}{{73}}\)
a) Phân số nào tối giản ? Vì sao ?
b) Phân số nào rút gọn được ? Hãy rút gọn phân số đó.
Hướng dẫn giải:
Cách rút gọn phân số :
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
a) Các phân số tối giản là : \(\frac{1}{3};\frac{4}{7};\frac{{72}}{{73}}\)
Vì tử số và mẫu số của mỗi phân số trên không cùng chia hết cho một số tự nhiên nào khác 1.
b) Các phân số rút gọn được là : \(\frac{8}{{12}};\frac{{30}}{{36}}\).
\(\frac{8}{{12}} = \frac{{8:4}}{{12:4}} = \frac{2}{3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{30}}{{36}} = \frac{{30:6}}{{36:6}} = \frac{5}{6}\)
Bài 3: Viết số thích hợp vào ô trống
Hướng dẫn giải:
Cách rút gọn phân số :
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
\(\begin{array}{l}
\frac{{54}}{{72}} = \frac{{54:2}}{{72:2}} = \frac{{27}}{{36}};\\
\frac{{27}}{{36}} = \frac{{27:3}}{{36:3}} = \frac{9}{{12}};\\
\frac{9}{{12}} = \frac{{9:3}}{{12:3}} = \frac{3}{4}.
\end{array}\)
Vậy ta có kết quả như sau :
1.3. Giải bài tập Sách giáo khoa Luyện tập trang 114
Bài 1: Rút gọn các phân số : \(\frac{{14}}{{28}};\frac{{25}}{{50}};\frac{{48}}{{30}};\frac{{81}}{{54}}\)
Hướng dẫn giải:
Cách rút gọn phân số :
- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.
- Chia tử số và mẫu số cho số đó.
Cứ làm như thế cho đến khi nhận được phân số tối giản (phân số không thể rút gọn được nữa).
\(\begin{array}{l}
\frac{{14}}{{28}} = \frac{{14:14}}{{28:14}} = \frac{1}{2};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{25}}{{50}} = \frac{{25:25}}{{50:50}} = \frac{1}{2};\\
\frac{{48}}{{30}} = \frac{{48:6}}{{30:6}} = \frac{8}{5};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{{81}}{{54}} = \frac{{81:9}}{{54:9}} = \frac{9}{6} = \frac{{9:3}}{{6:3}} = \frac{3}{2}.
\end{array}\)
Bài 2: Trong các phân số dưới đây, phân số nào bằng \(\frac{2}{3}\) ?
\(\frac{{20}}{{30}};\frac{8}{9};\frac{8}{{12}}\)
Hướng dẫn giải:
- Rút gọn các phân số thành phân số tối giản (nếu được). Các phân số cùng phân số tối giản thì bằng nhau.
\(\frac{{20}}{{30}} = \frac{{20:10}}{{30:10}} = \frac{2}{3};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\frac{8}{{12}} = \frac{{8:4}}{{12:4}} = \frac{2}{3}\)
\(\frac{8}{9}\) là phân số tối giản.
Vậy có 2 phân số bằng \(\frac{2}{3}\) là \(\frac{{20}}{{30}};\frac{8}{{12}}\).
Bài 3: Trong các phân số dưới đây, phân số nào bằng \(\frac{{25}}{{100}}\) ?
\(\frac{{50}}{{150}} ;\frac{5}{{20}};\frac{8}{{32}}\)
Hướng dẫn giải:
- Rút gọn các phân số thành phân số tối giản (nếu được). Các phân số cùng phân số tối giản thì bằng nhau.
Ta có : \(\frac{{25}}{{100}} = \frac{{25:25}}{{100:25}} = \frac{1}{4}\)
\(\frac{{50}}{{150}} & = \frac{{50:50}}{{150:50}} = \frac{1}{3};\,\,\,\,\,\,\,\,\,\,\,\,\frac{5}{{20}} = \frac{{5:5}}{{20:5}} = \frac{1}{4};\,\,\,\,\,\,\,\,\,\,\,\frac{8}{{32}} = \frac{{8:8}}{{32:8}} = \frac{1}{4}\)
Vậy các phân số bằng \(\frac{{25}}{{100}}\) là \(\frac{5}{{20}};\frac{8}{{32}}\).
Bài 4: Tính (theo mẫu)
a) \(\frac{{2 \times 3 \times 5}}{{3 \times 5 \times 7}}\); b) \(\frac{{8 \times 7 \times 5}}{{11 \times 8 \times 7}}\); c) \(\frac{{19 \times 2 \times 5}}{{19 \times 3 \times 5}}\);
Mẫu : a)
Chú ý : Trong mẫu trên, ta đã cùng chia nhẩm tích ở trên và tích ở dưới gạch ngang cho 3, rồi cùng chia nhẩm cho 5.
Hướng dẫn giải:
- Cùng chia nhẩm tích ở trên và tích ở dưới gạch ngang cho các thừa số chung.
Hỏi đáp về Rút gọn phân số
Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.
Copyright © 2021 HOCTAP247

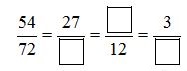
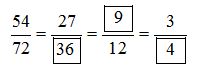
.PNG)
.PNG)