Hình thoi - Diện tích hình thoi

Hình thoi ABCD có :

• Cạnh AB song song với cạnh DC.

     Cạnh AD song song với cạnh BC.

• AB = BC = CD = DA.

Hình thoi có hai cặp cạnh đối diện song song và bốn cạnh bằng nhau.

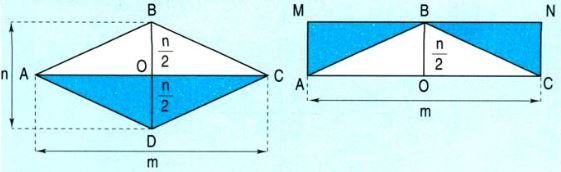
Cho hình thoi ABCD có AC = m, BD = n.

Cắt hình tam giác AOD và hình tam giác COD rồi ghép với hình tam giác ABC để được hình chữ nhật MNCA (xem hình vẽ).

Dựa vào hình vẽ ta có :

Diện tích hình thoi ABCD bằng diện tích hình chữ nhật MNCA.

Diện tích hình chữ nhật MNCA là \(m \times \frac{n}{2}\). Mà \(m \times \frac{n}{2} = \frac{{m \times n}}{2}\).

Vậy diện tích hình thoi ABCD là \(\frac{{m \times n}}{2}\)..

Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho 2 (cùng một đơn vị đo).

\(S=\frac{{m \times n}}{2}\).

(S là diện tích của hình thoi và m ; n là độ dài của hai đường chéo).

Bài 1: Trong các hình dưới đây

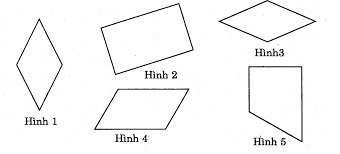
Hình nào là hình thoi ?

Hình nào là hình chữ nhật ?

Hướng dẫn giải:

• Quan sát hình vẽ để xác định tên của các hình đã cho.
• Hình thoi có hai cặp cạnh đối diện song song với bốn cạnh bằng nhau.

Hình 1, Hình 3 là hình thoi.

Hình 2 là hình chữ nhật.

Nói thêm : Hình 4 là hình bình hành, hình 5 là hình thang vuông.

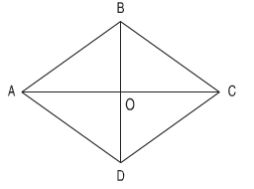
Bài 2: Trong hình thoi ABCD, AC và BD là hai đường chéo của hình thoi chúng cắt nhau tại điểm O.

a) Dùng ê ke để kiểm tra xem hai đường chéo có vuông góc với nhau hay không.

b) Dùng thước có vạch chia xăng-ti-mét để kiểm tra xem hai đường chéo có cắt nhau tại trung điểm của mỗi đường hay không.

 

Hướng dẫn giải:

• Dùng thước kẻ và ê ke đẻ kiểm tra theo yêu cầu của đề bài.

a) Kiểm tra sẽ thấy hai đường chéo vuông góc nhau.

b) Hai đường chéo cắt nhau tại trung điểm của mỗi đường vì khi kiểm tra ta thấy :

        OA = OC = 3cm  ;    OB = OD = 2cm.

Nhận xét : Hình thoi có hai đường chéo vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường.

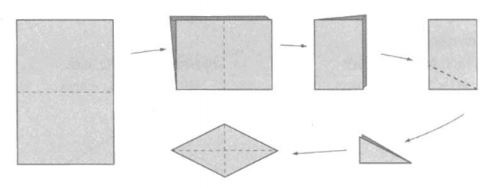
Bài 3: Thực hành gấp và cắt giấy (theo hình vẽ)  để tạo thành hình thoi.

Hướng dẫn giải:

• Học sinh quan sát và thực hành theo hình vẽ.

Học sinh xem kỹ hình vẽ để hiểu rõ bài và thực hành theo hình vẽ.

1.4. Giải bài tập Sách giáo khoa trang 142, 143

Bài 1: Tính diện tích của

a) Hình thoi ABCD, biết AC = 3cm, BD = 4cm.

b) Hình thoi MNPQ, biết MP = 7cm, NQ = 4cm.

Hướng dẫn giải:

Diện tích hình thoi bằng tích của độ dài hai đường chéo chia cho 2 (cùng đơn vị)

         \(S = \frac{{m \times n}}{2}\)  hoặc S = m × n : 2

(S là diện tích của hình thoi; m , n là độ dài của hai đường chéo).  

a) Diện tích hình thoi ABCD là :

               \(\frac{{3 \times 4}}{2} = \frac{{12}}{2} = 6\left( {c{m^2}} \right)\)

b) Diện tích hình thoi MNPQ là :

               \(\frac{{7 \times 4}}{2} = \frac{{24}}{2} = 14\left( {c{m^2}} \right)\)

Bài 2: Tính diện tích hình thoi biết

a) Độ dài các đường chéo là 5dm và 20dm;

b) Độ dài các đường chéo là 4m và 15dm.

Hướng dẫn giải:

• Nếu độ dài hai đường chéo chưa cùng đơn vị đo thì ta đổi về cùng đơn vị đo, sau đó để tính diện tích hình thoi ta lấy tích của độ dài hai đường chéo chia cho 2. 

a) Diện tích hình thoi là :

              \(\frac{{5 \times 20}}{2} = \frac{{100}}{2} = 50\left( {d{m^2}} \right)\)

b) Đổi :  4m = 40dm

Diện tích hình thoi là:

               \(\frac{{40 \times 15}}{2} = \frac{{600}}{2} = 300\left( {d{m^2}} \right)\)

Bài 3: Đúng ghi Đ, sai ghi S

a) Diện tích hình thoi bằng diện tích hình chữ nhật.                          

b) Diện tích hình thoi bằng \(\frac{1}{2}\) diện tích hình chữ nhật.    

Hướng dẫn giải:

• Để tính diện tích hình thoi ta lấy tích của độ dài hai đường chéo chia cho 2 (cùng một đơn vị đo). 
• Để tính diện tích hình chữ nhật ta lấy chiều dài nhân với chiều rộng.

Diện tích hình thoi là: 

               5 × 2 : 2 = 5 (cm²)

Diện tích hình chữ nhật là :

               5 × 2 = 10 (cm²)

Ta có :     10 : 5 = 2

Vậy diện tích hình chữ nhật gấp 2 lần diện tích hình thoi, hay diện tích hình thoi bằng \(\frac{1}{2}\) diện tích hình chữ nhật.

a) Ghi S vào ô trống.

b) Ghi Đ vào ô trống.

Nếu có thắc mắc cần giải đáp các em có thể để lại câu hỏi trong phần Hỏi đáp, cộng đồng Toán HOCTAP247 sẽ sớm trả lời cho các em.