Đề kiểm tra 45 phút - Đề số 3 - Chương 1 - Hình học 9

Đề bài

Bài 1. Không dùng bảng và máy tính, hãy tính:

\(A = {\sin ^2}10^\circ  + {\sin ^2}20^\circ  + ... + {\sin ^2}70^\circ  \)\(\;+ {\sin ^2}80^\circ \)

Bài 2. Cho tam giác ABC vuông tại A, biết \(AC = 12cm, BC = 15cm.\)

a. Giải tam giác vuông ABC.

b. Tính độ dài đường cao AH và đường phân giác AD của ∆ABC (số đo góc làm tròn đến độ, độ dài đoạn thẳng làm tròn đến chữ số thập phân thứ hai)

Bài 3. Cho hình bình hành ABCD có BD vuông góc với BC. Biết \(AB = a\), \(\widehat A = \alpha .\) Tính diện tích hình bình hành ABCD theo a và α.

Bài 4. Dựng góc \(α\), biết \(\tan α = 0,75\) (vẽ hình và nêu cách dựng).

Hướng dẫn giải

Bài 1. Ta có:

\(\eqalign{  & A = {\sin ^2}10^\circ  + {\sin ^2}20^\circ  + {\sin ^2}30^\circ  + {\sin ^2}40^\circ  + {\sin ^2}50^\circ  + {\sin ^2}60^\circ  + {\sin ^2}70^\circ  + {\sin ^2}80^\circ   \cr  &  = \left( {{{\sin }^2}10^\circ  + {{\sin }^2}80^\circ } \right) + \left( {{{\sin }^2}20^\circ  + {{\sin }^2}70^\circ } \right) + \left( {{{\sin }^2}30^\circ  + {{\sin }^2}60^\circ } \right) + \left( {{{\sin }^2}40^\circ  + {{\sin }^2}50^\circ } \right)  \cr  &  = \left( {{{\sin }^2}10^\circ  + {{\cos }^2}10^\circ } \right) + \left( {{{\sin }^2}20^\circ  + {{\cos }^2}20^\circ } \right) + \left( {{{\sin }^2}30^\circ  + {{\cos }^2}30^\circ } \right) + \left( {{{\sin }^2}40^\circ  + {{\cos }^2}40^\circ } \right)  \cr  &  = 1 + 1 + 1 + 1 = 4 \cr} \)

Bài 2. a. Ta có:

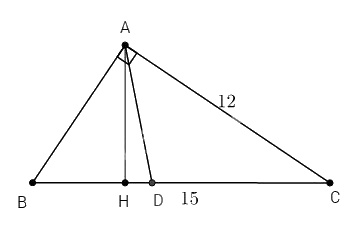
\(\eqalign{  & AB = \sqrt {B{C^2} - A{C^2}}  = \sqrt {{{15}^2} - {{12}^2}}  = 9\,\left( {cm} \right)  \cr  & \sin B = {{AC} \over {BC}} = {{12} \over {15}} = {4 \over 5} \Rightarrow \widehat B \approx 53^\circ  \cr} \)

Do đó: \(\widehat C \approx 90^\circ  - 53^\circ  = 37^\circ \)

b. ∆ABC vuông có đường cao AH, ta có:
AH.BC = AB.AC (định lí 3)

\( \Rightarrow AH = {{AB.AC} \over {BC}} = {{9.12} \over {15}} = 7,2\,\left( {cm} \right)\)

AD là phân giác của ∆ABC (gt)

\(\widehat {BAD} = \widehat {DAC} = {{\widehat {BAC}} \over 2} = {{90^\circ } \over 2} = 45^\circ \)

Lại có: \(\widehat {HAC} = \widehat B \approx 53^\circ \) (cùng phụ với góc C)

\( \Rightarrow \widehat {HAD} = \widehat {HAC} - \widehat {DAC} \approx 53^\circ  - 45^\circ  = 8^\circ \)

Xét tam giác vuông AHD ta có:

\(AH = AD.\cos \widehat {HAD} \Rightarrow AD = {{AH} \over {\cos \widehat {HAD}}} = {{7,2} \over {\cos 8^\circ }} \approx 7,27cm.\)

Bài 3.

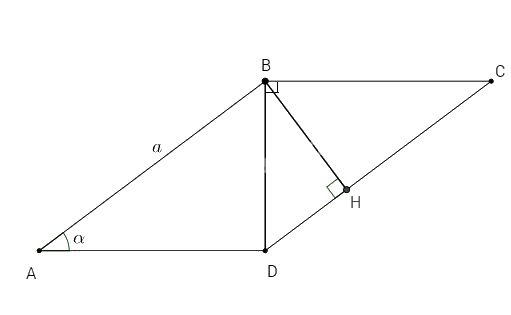
ABCD là hình bình hành nên \(\widehat C = \widehat A = \alpha \) và \(DC = AB = a\)

Ta có: ∆BDC vuông tại B (gt) nên \(BC = DC.\cosα = a.\cosα\)

Kẻ đường cao BH của tam giác BDC,

ta có ∆BHC vuông tại H:

\(BH = BC.\sin C  = a.\cosα.\sinα.\)

Do đó: \({S_{ABCD}} = DC.BH \)\(\;= a.a.\cos \alpha .\sin \alpha  = {a^2}.cos\alpha .sin\alpha \) (đvdt)

Bài 4.

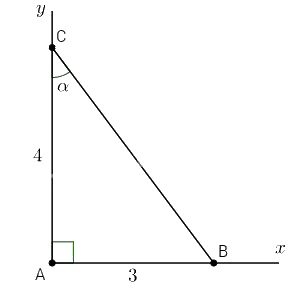
\(\tan \alpha  = 0,75 = {3 \over 4}\)

- Dựng góc vuông \(\widehat {xAy}\)

- Trên tia Ax lấy \(AB = 3.\)

- Trên tia Ay lấy \(AC = 4.\)

- Nối B với C

Ta được góc ACB là góc \(α\) cần dựng.