Giải bài 36 trang 94 - Sách giáo khoa Toán 9 tập 1

Đề bài

    Cho tam giác có một góc bằng 45o. Đường cao chia một cạnh kề với góc đó thành các phần 20cm và 21 cm. Tính cạnh lớn trong hai cạnh còn lại.    

Hướng dẫn giải

Giải: 

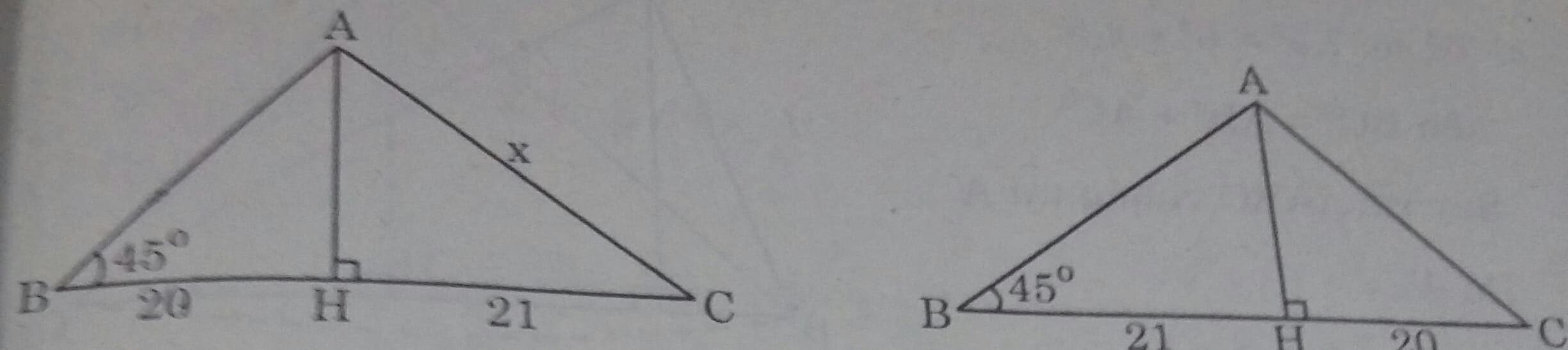
   Trong hình 46( SGK trang 94)

  Ta có HC > HB \( \Rightarrow AC> AB\). Tính AC.

 Xét tam giác vuông AHB có:

  AH= BH.tgB = 20.\(tg 45^0\)= 20.

  Áp dụng định lý Py- ta- go cho tam giác vuông AHC, ta được:

  \(AC= \sqrt{HA^2+ HC^2}=\sqrt{20^2+21^2}=29\)

 Trong hình 47( SGK trang 94) 

  Ta có: HB>HC \( \Rightarrow AB>AC. \ Tính \ AB.\)

   Xét tam giác vuông AHB có: 

   \(A= \frac{AH}{cosB}=\frac{21}{cos45^0}=21 \sqrt{2}\)